Prüfung 2023

Analysis, Teil 1

Aufgabe 1

Gegeben ist die Funktion \(g\) mit dem Term \(g(x)=-\frac{1}{4}x^{4}+2x^{2}\) und der Definitionsmenge \(D_{g}=[-3;3]\) . Der Graph von \(g\) wird mit \(G_{g}\) bezeichnet.

Aufgabe (a)

Untersuchen Sie \(G_{g}\) auf Symmetrie zum Koordinatensystem. [2]

---

Tipp

Wir berechnen \(g(-x)\) .

Aufgabe (b)

Ermitteln Sie alle Extremstellen von \(g\) . [4]

---

Tipp

Wir denken hier auch an die Randwerte.

Aufgabe 2

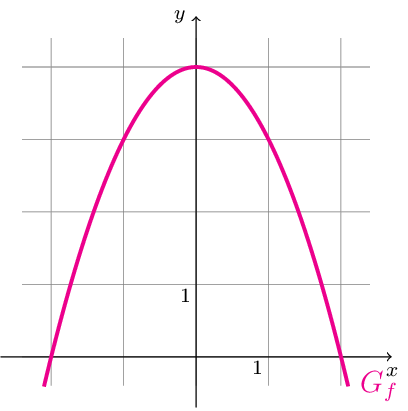
Die folgende Abbildung zeigt einen Ausschnitt des Graphen \(G_{f}\) der Funktion \(f\) mit dem Definitionsbereich \(D_{f}=\mathbb{R}\) . Die Funktion \(f\) ist eine quadratische Funktion.

Aufgabe (a)

\(G_{f}\) und die \(x\)-Achse schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. [4]

---

Tipp

Wir bestimmen zu erst den Term \(f(x)\) .

Ergebnis

\(A=\frac{32}{3}\)

Aufgabe (b)

Die Funktion \(F\) ist eine Stammfunktion von \(f\) und ihr Graph wird mit \(G_{F}\) bezeichnet. Beschreiben Sie den Globalverlauf von \(G_{F}\) in Worten. Gehen Sie auch auf das Monotonieverhalten, die Lage und die Art der Extremstellen sowie auf die Lage der Wendestelle von \(F\) ein. [4]

---

Tipp

• \(F^{\prime}(x)=f(x)\) und damit können wir die Monotonie von \(G_{F}\) angeben.

• Wir formulieren zu erst die Monotonie und folgern daraus auf den Globalverlauf.

Aufgabe 3

Lösen Sie die Gleichung \((e^{x})^{2}-25=0\) über der Grundmenge der reellen Zahlen. [3]

---

Ergebnis

\(x=\ln5\)

Aufgabe 4

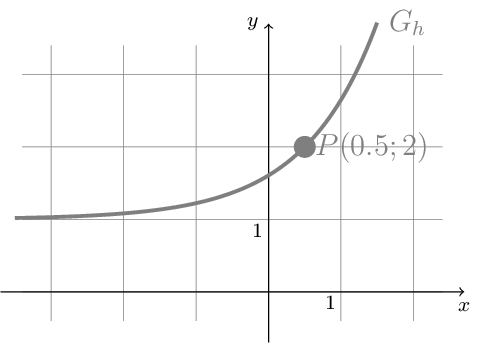
Die folgende Abbildung zeigt einen Ausschnitt des Graphen \(G_{h}\) einer Exponentialfunktion h mit der Definitionsmenge \(D_{h}=\mathbb{R}\) . Der zugehörige Funktionsterm besitzt die Form \(h(x)=e^{x+d}+y_{0}\) .

Aufgabe (a)

Bestimmen Sie mithilfe der obigen Abbildung nachvollziehbar die Werte der Parameter \(d\) und \(y_{0}\) . [3]

---

Tipp

Wir betrachten den Grenzwert \(\underset{x\rightarrow-\infty}{\lim}h(x)\) .

Aufgabe (b)

Entscheiden Sie anhand des Graphen \(G_{h}\) , ob die Aussage \(\int\limits_{-1}^{1}(2-h(x))dx>0\) wahr oder falsch ist. Veranschaulichen Sie Ihre Überlegungen dazu in der Abbildung. [2]

---

Tipp

Wir markieren zwei geeignete Flächen in der Skizze.

Stochastik, Teil 1

Aufgabe 1

Bei einem Glücksradspiel beträgt der Einsatz \(2\) € , maximal werden \(5\) € ausbezahlt. Die Zufallsgröße \(X\) gibt den Nettogewinn bei diesem Spiel (in Euro) an. Die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) kann mithilfe der Parameter \(a\) und \(b\) in einer Tabelle dargestellt werden.

\(x\)	\(\;\small{-2}\)	\(\;\small{-1}\)	\(\;\small{0.5}\)	\(\;\small{1.5}\)	\(\;\small{3}\)
\(P(X=x)\)	\(\small{0.20}\)	\(\small{a}\)	\(\small{0.20}\)	\(\small{b}\)	\(\small{0.10}\)

Aufgabe (a)

Erläutern Sie, was der Ausdruck „faires Spiel“ im Zusammenhang mit Glücksspielen bedeutet und nennen Sie eine Bedingung, die von der hier dargestellten Zufallsgröße \(X\) erfüllt werden muss, damit das beschriebene Glücksspiel fair ist. [2]

Aufgabe (b)

Berechnen Sie die Werte der Parameter \(a\) und \(b\) so, dass es sich bei diesem Glücksradspiel um ein faires Spiel handelt. [4]

Aufgabe 2

Ein Gaststättenverband hat unter \(1500\) Touristen in der Fränkischen Schweiz eine Befragung durchgeführt, um zu erfahren, ob die Touristen die heimischen Biergärten besuchen (\(B\)) . Dabei wurde zwischen Personen, die eine Tagestour bei einem Veranstalter gebucht haben (\(V\)) , und Individualtouristen (\(\overline{V}\)) unterschieden. Tausend der Befragten gaben an, keine Tagestour bei einem Veranstalter gebucht zu haben. Von den Touristen, die sich für eine Tagestour entschieden hatten, besuchten \(80~\%\) einen Biergarten. Nur \(300\) aller Befragten gaben an, keinen Biergarten besucht zu haben. Relative Häufigkeiten werden als Wahrscheinlichkeiten interpretiert.

Aufgabe (a)

Bestimmen Sie mithilfe einer vollständig ausgefüllten Vierfeldertafel den Anteil der Touristen, die entweder eine Tagestour bei einem Veranstalter gebucht haben oder einen Biergarten in der Fränkischen Schweiz besucht haben. [4]

---

Tipp

Wir tragen die absoluten Häufigkeiten in die Vierfeldertafel ein und berechnen anschließend die nötigen relativen Häufigkeiten.

Aufgabe (b)

Begründen Sie, ob der Gaststättenverband mit der folgenden Behauptung recht hat: „Die Biergärten in der Fränkischen Schweiz sind für alle Touristen gleich attraktiv, egal ob zuvor eine Tagestour bei einem Veranstalter gebucht wurde oder nicht“. [2]

---

Tipp

Wir untersuchen zwei geeignete Ereignisse auf stochastische Unabhängigkeit.

Analysis, Teil 2.1

Aufgabe 1

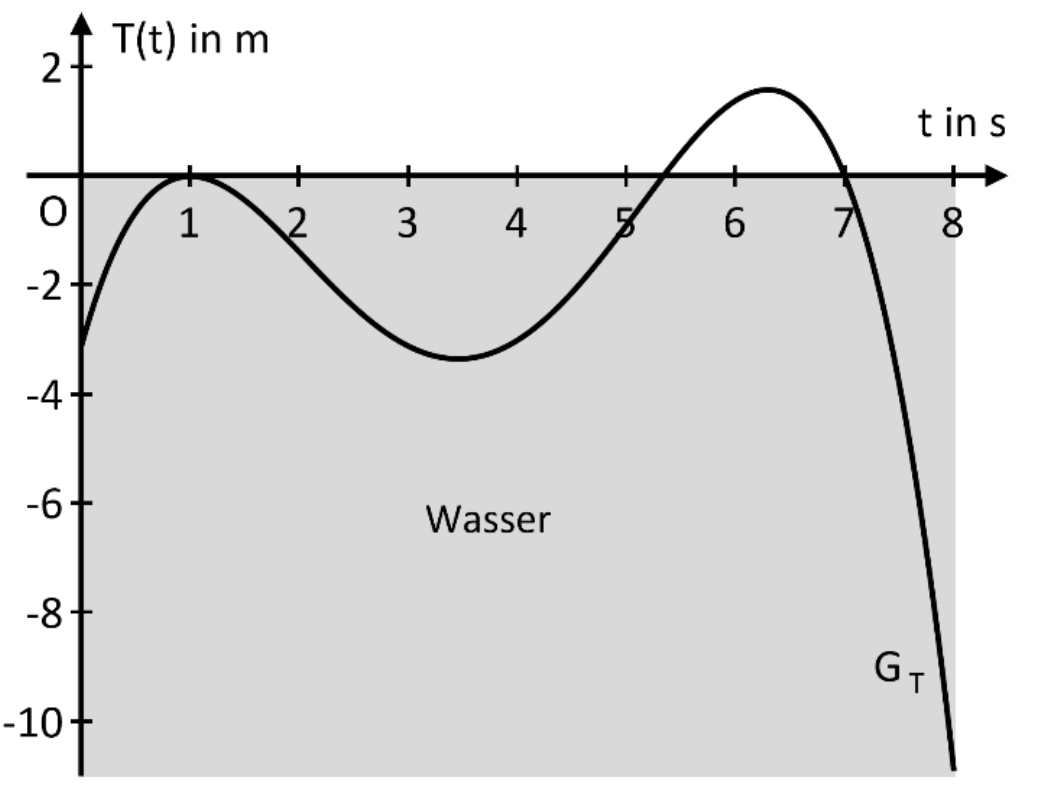
Das Auf- und Abtauchverhalten eines Delfins im Meer wird mittels eines an ihm angebrachten Sensors untersucht. Die momentane Höhe des Sensors in Metern bezogen auf die Wasseroberfläche in Abhängigkeit von der Zeit \(t\) in Sekunden lässt sich annähernd durch die Funktionswerte der Funktion \(T\) beschreiben. Der Graph der Funktion \(T\) wird mit \(G_{T}\) bezeichnet und ist im Zeitraum von \(0\) bis \(8\) Sekunden im folgenden Koordinatensystem abgebildet. Die Funktion \(T\) ist eine ganzrationale Funktion vierten Grades und zum Zeitpunkt \(t_{1}=1\) befindet sich der Delfin an der Wasseroberfläche. Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Aufgabe (a)

Beschreiben Sie anhand des Funktionsgraphen \(G_{T}\) den Bewegungsablauf des Delfins im Bereich von \(t=5.3\) bis \(t=7\) und erläutern Sie, ob für die Funktion \(T\) das Intervall \([0;+\infty[\) für den beschriebenen Sachverhalt eine sinnvolle Definitionsmenge ist. [2]

Aufgabe (b)

Der Leitkoeffizient im Funktionsterm von \(T\) ist gegeben durch \(a=-\frac{1}{12}\) . Zudem ist bekannt, dass \(G_{T}\) den Schnittpunkt \(S(0;-\frac{28}{9})\) mit der Ordinatenachse besitzt. Die zwei ganzzahligen Nullstellen von \(T\) können der Zeichnung entnommen werden. Berechnen Sie den exakten Wert der fehlenden Nullstelle von \(T\) . [4]

---

Tipp

Wir geben als Ansatz die Linearfaktorenzerlegung von \(T(t)\) an.

Aufgabe (c)

Die Funktion \(T\) ist gegeben durch den Term \(T(t)=-\frac{1}{12}(t^{4}-\frac{43}{3}t^{3}+63t^{2}-87t+\frac{112}{3})\) mit dem Definitionsbereich \(D_{T}=[0;8]\) . Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.

1. Bestimmen Sie die Wertemenge \(W_{T}\) der Funktion \(T\) und interpretieren Sie diese im Sachzusammenhang. [9]

---

Tipp

Wir berechnen die Koordinaten der Extrempunkte von \(G_{T}\) und vergessen die Randwerte nicht.

2. Für \(t\in]1;5.3[\) befindet sich der Delfin unter Wasser. Ermitteln Sie rechnerisch, ob in diesem Zeitintervall der Betrag der größten Abtauchgeschwindigkeit größer als der Betrag der größten Auftauchgeschwindigkeit ist. [6]

---

Tipp

Wir berechnen die Steigung von \(G_{T}\) in den beiden Wendpunkten.

Aufgabe 2

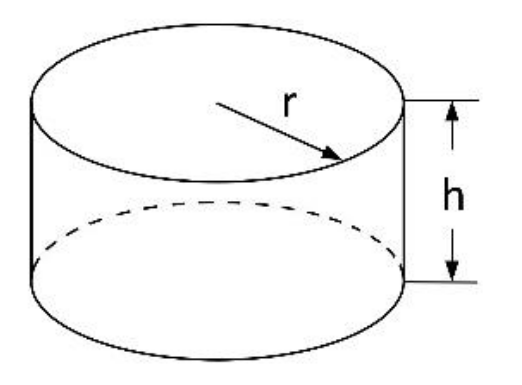
An einem Küstenabschnitt stranden immer wieder Delfine. Diese werden in einer Auffangstation gesund gepflegt, bis sie wieder in freier Natur überleben können. Um die Kapazität der Auffangstation zu erhöhen, soll ein zusätzliches Becken aus Edelstahl angefertigt werden, welches die Form eines geraden Kreiszylinders hat und nach oben offen ist. Dazu steht ein begrenzter Vorrat an Edelstahlblechen zur Verfügung. Diese haben modellhaft insgesamt eine Fläche von \(180\pi\,\mathrm{m^{2}}\) . Aus Platzgründen kann das Becken nur einen maximalen Durchmesser von \(20\,\mathrm{m}\) haben. Die Funktion \(V\) mit dem Term \(V(r)\) beschreibt die Maßzahl des Volumens des Beckens in Kubikmetern in Abhängigkeit vom Radius \(r\) in Metern. Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf eine Nachkommastelle.

Aufgabe (a)

Stellen Sie eine Gleichung der Funktion \(V\) auf. Begründen Sie, dass \(D_{V}=]0;10]\) die mathematisch maximale Definitionsmenge von \(V\) ist . [5]

---

Tipp

Zur Herleitung nehmen wir die Formeln für Volumen und Oberfläche des Zylinders.

Ergebnis

\(V(r)=-\frac{1}{2}\pi\cdot r^{3}+90\pi\cdot r\)

Aufgabe (b)

Zeigen Sie, dass unter den oben genannten Vorgaben das Becken für einen Radius von \(r=2\sqrt{15}\) den maximalen Rauminhalt aufweist. Überprüfen Sie anschließend, ob dieses Becken für eine vorübergehende Haltung von drei Delfinen ausreicht, wenn pro Delfin \(360\,\mathrm{m^{3}}\) Wasser zur Verfügung stehen sollen. [7]

---

Tipp

Es liegt eine klassische Extremwertaufgabe vor.

Aufgabe (c)

Berechnen Sie für den Beckenradius \(r=2\sqrt{15}\) die Größe der Grundfläche des Beckens \(A_{0}\) in Quadratmetern. [2]

---

Ergebnis

\(A_{0}\approx188.5\,\mathrm{m^{2}}\)

Aufgabe (d)

Ein zu Beginn (Zeitpunkt \(t_{0}=0\)) \(0.5\,\mathrm{m^{2}}\) großer Algenteppich, der sich am Boden des Beckens mit der Grundfläche \(A_{0}=188.5\,\mathrm{m^{2}}\) gebildet hat, verdoppelt seine Fläche täglich.

1. Stellen Sie eine Gleichung der Funktion \(A\) mit dem Term \(A(t)\) auf, welche die Fläche des Algenteppichs in Quadratmetern in Abhängigkeit von der Zeit \(t\) in Tagen angibt. Für die Definitionsmenge der Funktion \(A\) gilt \(D_{A}=[0;8]\) . [2]

2. Zeigen Sie, dass sich die Wachstumsfunktion \(A\) näherungsweise durch die Funktionsgleichung \(\widetilde{A}(t)=0.5\cdot e^{0.6931\cdot t}\) mit \(t\in[0;8]\) darstellen lässt und berechnen Sie damit, nach wie vielen Tagen zwei Drittel der gesamten Grundfläche des Beckens von Algen bedeckt wären, wenn nicht eingegriffen würde. Runden Sie Ihr Ergebnis auf ganze Tage. [6]

Analysis, Teil 2.2

Aufgabe 1

Der Graph der Funktion \(f\) mit der Definitionsmenge \(D_{f}=\mathbb{R}\) schneidet in einem kartesischen Koordinatensystem die \(y\)-Achse beim Wert \(y=2\) und verläuft durch den Extrempunkt \(E(2;1.2)\) . Außerdem ist bekannt, dass der Funktionsterm durch \(f(x)=ax^{3}+bx^{2}-0.9x+c\) mit \(a,b,c\in\mathbb{R}\) dargestellt werden kann.

Aufgabe (a)

Bestimmen Sie im Funktionsterm von \(f\) die Werte der Parameter \(a\), \(b\) und c . [6]

---

Ergebnis

\(f(x)=-0.025x^{3}+0.3x^{2}-0.9x+2\)

Aufgabe (b)

Im Folgenden wird die Funktion \(g\) mit \(g(x)=f(x)=-0.025(x^{3}-12x^{2}+36x-80)\) und \(D_{g}=[0;7]\) betrachtet. Der Graph von \(g\) wird mit \(G_{g}\) bezeichnet.

1. Bestimmen Sie jeweils die Art und die Koordinaten aller Extrempunkte von \(G_{g}\) und geben Sie die Wertemenge \(W_{g}\) von \(g\) an. [9]

---

Tipp

Auch hier beachten wir die Randwerte.

2. Zeichnen Sie den Graphen \(G_{g}\) unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte für \(0\leq x\leq7\) in ein Koordinatensystem. Maßstab für die \(x\)-Achse: \(1\,\mathrm{LE}=1\,\mathrm{cm}\) , für die \(y\)-Achse: \(1\,\mathrm{LE=2\,\mathrm{cm}}\) . [4]

---

Tipp

Wir erstellen eine Wertetabelle.

3. Der Graph \(G_{g}\) , die \(x\)-Achse und die Senkrechten mit den Gleichungen \(x=2\) und \(x=6\) schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks. [3]

Aufgabe 2

Beim Aufladen des Akkus eines Smartphones fließt ein Ladestrom von \(2000\) Milliampere. Sobald der Akku optimal geladen ist, verringert das Ladegerät den Ladestrom um eine Überladung zu vermeiden.

Die Funktion \(I\) mit dem Term \(I(t)=2000\cdot0.5^{\frac{t}{4.88}}\) und \(t\geq0\) modelliert den Verlauf des Ladestroms ab dem Erreichen der optimalen Akkuladung zur Zeit \(t=0\) bis zur endgültigen Abschaltung des Ladegeräts zur Zeit \(t_{end}\geq0\) . Die Funktionswerte von \(I\) entsprechen der Stärke des Ladestroms in Milliampere und \(t\) entspricht der Zeit in Minuten. Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.

Aufgabe (a)

Zeigen Sie, dass sich der Funktionsterm \(I(t)\) näherungsweise auch in der Form \(\widetilde{I}(t)=2000\cdot e^{-0.142\cdot t}\) schreiben lässt. [3]

---

Tipp

Wir ersetzen \(0.5\) mit \(e^{\ln0.5}\) .

Aufgabe (b)

Das Ladegerät schaltet sich komplett ab, wenn die Ladestromstärke auf \(100\) Milliampere abgesunken ist. Ermitteln Sie \(t_{end}\) . Runden Sie das Ergebnis auf ganze Minuten und geben Sie eine sinnvolle Definitionsmenge für \(\widetilde{I}\) an. [4]

Aufgabe 3

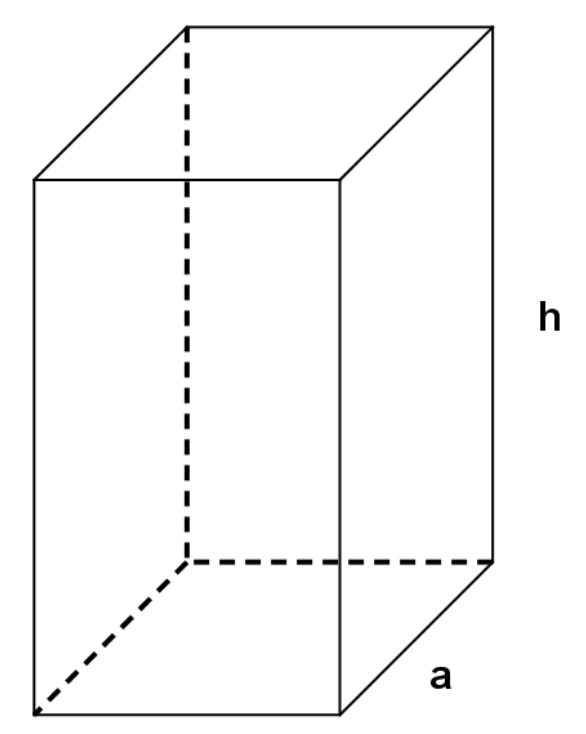
Die Firma FACTUS soll für einen Süßwarenhersteller quaderförmige Verpackungen für Schokoladenbonbons produzieren. Der Auftraggeber verlangt, dass die Verpackung eine quadratische Grundfläche aufweist und dass die Summe aus Länge, Breite und Höhe \(45\,\mathrm{cm}\) beträgt, damit der Verpackungsautomat die gefalteten Verpackungen verarbeiten und befüllen kann. Die Seitenlänge der quadratischen Grundfläche wird mit \(a\) bezeichnet. Die Werte der Funktion \(V\) mit dem Term \(V(a)\) geben jeweils das Volumen der Verpackung in \(\mathrm{cm^{3}}\) an. Damit die Verpackung handlich bleibt, soll die Seitenlänge a der Grundfläche mindestens \(10\,\mathrm{cm}\) und höchstens \(20\,\mathrm{cm}\) betragen. Bei den Berechnungen kann auf das Mitführen der Einheiten verzichtet werden.

Aufgabe (a)

Bestimmen Sie einen Funktionsterm \(V(a)\) der Funktion \(V\) . [3]

---

Tipp

Wir zählen Länge, Breite und Höhe eines Quaders zusammen.

Ergebnis

\(V(a)=45a^{2}-2a^{3}\)

Aufgabe (b)

Ermitteln Sie die Maße einer Verpackung der Firma FACTUS, die den Vorgaben entspricht und dabei maximales Volumen besitzt. Geben Sie die spezielle Form dieser Verpackung an und berechnen Sie das Volumen. [7]

---

Tipp

Wir haben hier eine klassische Extremwertaufgabe vorliegen.

Aufgabe (c)

Die Firma FACTUS bekommt den Auftrag, \(6000\) würfelförmige und bedruckte Verpackungen mit einer Kantenlänge von \(15\,\mathrm{cm}\) herzustellen. Aus Kostengründen überlegt die Firma, ob sie den Druckauftrag an die eigene Druckerei FACTUS-Print geben soll, oder ob das Angebot der Konkurrenzfirma PappDruck günstiger ist. Bei den Verpackungen werden alle Außenflächen außer der Bodenfläche bedruckt.

	Druckkosten	Rabatt
FACTUS	\(8\) Cent pro \(1000\,\mathrm{cm^{2}}\)	kein Rabatt
PappDruck	\(9\) Cent pro Verpackung	Bedruckung jedes 10. Würfels gratis

Entscheiden Sie rechnerisch, welche Firma aus wirtschaftlicher Sicht den Druckauftrag bekommen sollte. [4]

Stochastik, Teil 2.1

Aufgabe 1

Bei einem Hersteller von Elektroautos (E-Autos) können die Kunden beim Kauf eines Autos zwischen den Modellen \(A\), \(B\) und \(C\) wählen. \(30~\%\) der Kunden entscheiden sich für Modell \(C\) . Die restlichen Kunden wählen zu gleichen Teilen \(A\) bzw. \(B\) . Die Modelle \(B\) und \(C\) werden mit einer kleinen (\(K\)) oder einer großen (\(G\)) Batterie angeboten. Das Modell \(A\) kann nur mit einer kleinen Batterie bestellt werden. Bei Modell \(B\) entscheiden sich vier von zehn Kunden für die große Batterie, während sich beim Modell \(C\) nur \(15~\%\) der Kunden für die kleine Batterie entscheiden. Zusätzlich können alle Modelle noch mit einem Autopilot (\(P\)) ausgestattet werden. Bei Modell \(B\) und \(C\) erfolgt die Wahl unabhängig von der Batteriegröße. Dieses Zusatzangebot wählen beim Modell \(A\) \(20~\%\) der Kunden und beim Modell \(B\) jeweils \(30~\%\) . Insgesamt werden \(41.5~\%\) aller Fahrzeuge mit Autopilot gewünscht.

Die Wahl des Modells, der Batteriegröße und der Zusatzfunktion Autopilot eines beliebig herausgegriffenen Kunden wird als Zufallsexperiment aufgefasst.

Aufgabe (a)

Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller zehn Elementarereignisse des betrachteten Zufallsexperiments. [6]

---

Ergebnis

\(P(\{CKP\})=0.036\)

Aufgabe (b)

Wir betrachent zwei Ereignisse \(E_{1}\) und \(E_{2}\) .

\(E_{1}:~\)“Ein zufällig ausgewählter Kunde wählt Modell A oder C jeweils mit Autopilot.“

\(E_{2}:~\)“Ein zufällig ausgewählter Kunde wählt entweder die kleine Batterie oder den Autopilot.“

Berechnen Sie nachvollziehbar die Wahrscheinlichkeit für \(E_{1}\) und für \(E_{2}\) . [3]

Aufgabe 2

In einer Kleinstadt sind \(30~\%\) aller zugelassenen Elektroautos zum einen der Oberklasse (\(O\)) zuzuordnen, die restlichen werden zum anderen der Mittelklasse (\(M\)) zugeordnet. Die Akkus aller hier betrachteten Elektroautos werden zu \(39.5~\%\) regelmäßig über eine Photovoltaik-Anlage (\(V\)) des jeweiligen Fahrzeugeigners geladen. Die Wahrscheinlichkeit dafür, dass ein zufällig aus all diesen Fahrzeugen ausgewähltes Elektroauto ein Modell der Oberklasse ist und regelmäßig über eine Photovoltaik-Anlage aufgeladen wird, beträgt \(25.5~\%\) .

Aufgabe (a)

Erstellen Sie eine vollständig ausgefüllte Vierfeldertafel und berechnen Sie die Wahrscheinlichkeit des Ereignisses \(E_{3}=\overline{M\cap V}\) . [4]

Aufgabe (b)

Untersuchen Sie, ob der Anteil der Fahrzeuge, die über eine Photovoltaik-Anlage des Fahrzeugeigners geladen werden, bei den Oberklasse-Modellen höher ist als bei den Mittelklasse-Modellen. Entscheiden Sie anschließend, ob die Ereignisse \(M\) und \(V\) stochastisch unabhängig sind. [4]

Aufgabe 3

Am Parkplatz eines großen Einkaufszentrums wurde im Rahmen einer Bachelor-Arbeit eine lang angelegte Studie zum Laden von E-Autos an den dort vorhandenen Ladesäulen durchgeführt. Diese lieferte folgende Ergebnisse: \(80~\%\) der Ladevorgänge erfolgen während der Zeit, in der die Besitzer der Fahrzeuge im Einkaufszentrum verweilen. Alle anderen Besitzer verbringen die Ladezeit in den umliegenden kleineren Geschäften, Bars, Cafés oder im Biergarten. Zudem wurde festgestellt, dass \(5~\%\) aller auf dem Parkplatz parkenden PKW E-Autos sind.

Bestimmen Sie, basierend auf den Ergebnissen der Studie, die Wahrscheinlichkeiten der folgenden Ereignisse \(E_{4}\) , \(E_{5}\) und \(E_{6}\) . [6]

\(E_{4}:~\)“Unter elf Ladevorgängen erfolgen genau neun in der Zeit, in der die Besitzer der Fahrzeuge im Einkaufszentrum verweilen.“

\(E_{5}:~\)“Unter \(50\) Ladevorgängen erfolgen mehr als neun aber weniger als \(18\) in der Zeit, in der die Besitzer der Fahrzeuge nicht im Einkaufszentrum verweilen.“

\(E_{6}:~\)“Unter \(100\) auf dem Parkplatz parkenden Pkw sind mehr E-Autos als nach der Studie zu erwarten wären.“

Stochastik, Teil 2.2

Aufgabe 1

Am Pausenverkauf einer großen Mädchenschule kaufen an einem Tag erfahrungsgemäß \(30~\%\) aller Schülerinnen eine Breze. Es werden \(20\) Schülerinnen an einem bestimmten Tag zufällig ausgewählt. Die Zufallsgröße \(X\) gibt an, wie viele von diesen am betrachteten Tag eine Breze kaufen.

Aufgabe (a)

Berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse \(E_{1}\) und \(E_{2}\) . [3]

Aufgabe (b)

Berechnen Sie den Erwartungswert der Zufallsgröße \(X\) und interpretieren Sie diesen im Sachzusammenhang. [2]

Aufgabe (c)

Bestimmen Sie die Wahrscheinlichkeit, mit der die Zufallswerte von \(X\) innerhalb der einfachen Standardabweichung um den Erwartungswert liegen. [4]

Aufgabe (d)

Berechnen Sie die Wahrscheinlichkeit des Ereignisses \(E_{3}\) . [3]

\(E_{3}:~\)“Mehr als doppelt so viele Schülerinnen wie erwartet kaufen eine Breze.“

Aufgabe 2

In einer Urne befinden sich sechs grüne, eine rote und eine blaue Kugel. Ein Zufallsexperiment besteht darin, nacheinander jeweils zufällig eine Kugel ohne Zurücklegen zu ziehen und deren Farbe festzustellen. Es wird so lange gezogen, bis die blaue Kugel erscheint, höchstens jedoch dreimal.

Aufgabe (a)

Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller zehn Elementarereignisse des betrachteten Zufallsexperiments. [5]

Aufgabe (b)

Wir betrachten nun die Ereignisse \(A\) und \(B\) .

\(A:~\)“Es werden alle drei Farben gezogen.“

\(B:~\)“Das Zufallsexperiment endet mit dem Zug der blauen Kugel.“

Berechnen Sie nachvollziehbar die Wahrscheinlichkeiten für die Ereignisse \(A\) und \(B\) . [3]

---

Ergebnis

\(P(A)=\frac{1}{28}\) ; \(P(B)=\frac{3}{8}\)

Aufgabe (c)

Bestimmen Sie die Wahrscheinlichkeit dafür, dass insgesamt drei Kugeln gezogen werden unter der Bedingung, dass das Zufallsexperiment mit der blauen Kugel endet. [3]