Logarithmusfunktionen¶
Die natürliche Exponentialfunktion \(g:y=e^{x}\) hat den Definitionsbereich \(D_{g}=\mathbb{R}\) und den Wertebereich \(W_{g}=\mathbb{R}^{+}\). Außerdem ist der Graph der natürlichen Exponentialfunktion echt monoton steigend.
Stellen wir die Gleichung \(y=e^{x}\) nach \(x\) um, so erhalten wir die Beziehung \(x=\ln y\). Daraus definieren wir die natürliche Logarithmusfunktion.
Die natürliche Logarithmusfunktion hat den Wertebereich \(W_{f}=\mathbb{R}\).
Wir wählen \(a,b\in\mathbb{R}^{+}\) und weisen folgende Rechenregeln für den natürlichen Logarithmus nach.
\(\ln(a\cdot b)=\ln(a)+\ln(b)\)
\(a\cdot b=e^{\ln(a\cdot b)}\) , aber auch \(a\cdot b=e^{\ln(a)}\cdot e^{\ln(b)}=e^{\ln(a)+\ln(b)}\)
Somit erhalten wir \(e^{\ln(a\cdot b)}=e^{\ln(a)+\ln(b)}\) oder \(\ln(a\cdot b)=\ln(a)+\ln(b)\) .
\(\ln a^{b}=b\cdot\ln a\)
\(a^{b}=e^{\ln a^{b}}\) , aber auch \(a^{b}=\left(e^{\ln(a)}\right)^{b}=e^{\ln(a)\cdot b}=e^{b\cdot\ln(a)}\)
Somit erhalten wir \(e^{\ln a^{b}}=e^{b\cdot\ln(a)}\) oder \(\ln a^{b}=b\cdot\ln a\) .
\(\ln\frac{a}{b}=\ln a-\ln b\)
\(\ln\frac{a}{b}=\ln(a\cdot b^{-1})=\ln(a)+\ln(b^{-1})=\ln a-\ln b\)
\(\ln\sqrt[b]{a}=\frac{1}{b}\ln a\)
\(\ln\sqrt[b]{a}=\ln a^{\frac{1}{b}}=\frac{1}{b}\ln a\)
Basisumrechnung beim Logarithmus
\(a^{x}=b\Leftrightarrow x=\log_{a}b\)
\(\ln a^{x}=\ln b\) ; \(x\cdot\ln a=\ln b\) ; \(x=\frac{\ln b}{\ln a}\)
\(\log_{a}b=\frac{\ln b}{\ln a}\)
Somit können wir jede Logarithmusfunktion auf die natürliche Logarithmusfunktion zurückführen und die obigen Rechengesetze gelten dann auch für jede beliebige Logarithmusfunktion.
Zum Nachweis setzten wir \(e^{\ln x}=x\) und leiten beide Seiten ab.
\(\left(e^{\ln x}\right)^{\prime}=1\)
\(e^{\ln x}\cdot\left(\ln x\right)^{\prime}=1\)
\(x\cdot\left(\ln x\right)^{\prime}=1\)
\(\left(\ln x\right)^{\prime}=\dfrac{1}{x}\)
\(f^{\prime}(x)=\dfrac{1}{x}>0\) für alle \(x\in\mathbb{R}^{+}\). Die natürliche Logarithmusfunktion ist in \(\mathbb{R}^{+}\) differenzierbar und echt monoton zunehmend.
Die zweite Ableitung der natürlichen Logarithmusfunktion ist \(f^{\prime\prime}(x)=-\dfrac{1}{x^{2}}\) . Das bedeutet dass der Graph \(G_{f}\) der natürlichen Exponentialpunktion in \(\mathbb{R}^{+}\) rechtsgekrümmt ist und keine Extrem oder Wendepunkte hat.
Der Graph \(G_{f}\) der natürlichen Logarithmusfunktion entsteht durch Spiegelung von \(G_{g}\) an der Winkelhalbierenden des 1. und 3. Quadranten.
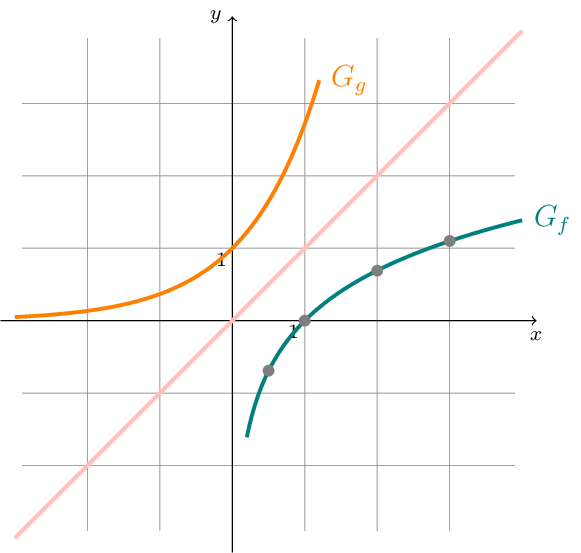
\(G_{f}\) schneidet die \(x\)-Achse im Punkt \(B(1;0)\) und für die Randwerte gilt
\(\underset{x\rightarrow\infty}{\lim}\left(\ln x\right)=\infty\) und \(\underset{x\rightarrow 0^{+}}{\lim}\left(\ln x\right)=-\infty\) .
Die \(y\)-Achse ist vertikale Asymptote von \(G_{f}\).
Das unbestimmte Integral der natürlichen Logarithmusfunktion bestimmen wir mit Hilfe der partiellen Integration.
Für zwei integrierbare Funktionen \(u\) und \(v\) gilt
\(\int\left(u(x)\cdot v^{\prime}(x)\right)dx=u(x)\cdot v(x)-\int\left(u^{\prime}(x)\cdot v(x)\right)dx+C\) .
\(\int\ln xdx=\int(1\cdot\ln x)dx\)
\(\qquad =x\cdot\ln x-\int x\cdot\dfrac{1}{x}dx\)
\(\qquad =x\cdot\ln x-\int1dx=x\cdot\ln x-x+C\)
\(\int\left[(ax+b)\cdot\ln(mx)\right]dx=(\frac{a}{2}x^{2}+bx)\cdot\ln(mx)-\int(\frac{a}{2}x^{2}+bx)\cdot\dfrac{1}{x}dx\)
\(\qquad =(\frac{a}{2}x^{2}+bx)\cdot\ln(mx)-\int(\frac{a}{2}x+b)dx\)
\(\qquad =(\frac{a}{2}x^{2}+bx)\cdot\ln(mx)-\frac{a}{4}x^{2}-bx+C\)
Bei der Kurvendiskussion von Exponential- und Logarithmusfunktionen treten die Funktionsterme in kombinierter Form auf. Der betrachtete Funktionsterm ist ein Produkt oder ein Quotient aus einem Exponential-, Logarithmus-, oder einem Polynomterm. Berechnen wir bei solchen zusammengesetzten Termen einen Grenzwert, so stehen Polynomfunktionen, \(e\)-Funktionen oder \(\ln\)-Funktionen in gegenseitiger Konkurrenz. Mit Hilfe der Prioritätsregeln können wir die Berechnung von Grenzwerten bei zusammengesetzten Funktionstermen leichter durchführen.