Punkte und Ortsvektoren¶

Aufgaben

Der dreidimensionale Raum, in dem wir uns bewegen und leben wird in der Geometrie Anschauungsraum genannt. Der Anschauungsraum besteht aus unendlich vielen Punkten. Die Menge all dieser Punkte wird mit \(\widetilde{P}\) bezeichnet. Zwei beliebige Punkte \(A\) und \(B\) aus \(\widetilde{P}\) bestimmen genau einen Vektor \(\overrightarrow{v}\), nämlich \(\overrightarrow{v}=\overrightarrow{AB}\). Der Vektor \(\overrightarrow{v}=\overrightarrow{AB}\) ist ein Element des dreidimensionalen Vektorraums \(\mathbb{R}^{3}\). Alle Vektoren, die aus den Punkten des Anschauungsraums gebildet werden, sind Elemente des dreidimensionalen Vektorraums \(\mathbb{R}^{3}\). Vorerst geht es darum, die Position der Punkte im Anschauungsraum \(\widetilde{P}\) in eindeutiger Weise durch Angabe von Zahlen eindeutig zu kennzeichnen.

Zunächst wird ein frei oder passend gewählter Punkt des Anschauungsraums \(\widetilde{P}\) ausgezeichnet. Wir nennen diesen Punkt Ursprung \(O\). Zum Ursprung \(O\) nimmt man eine beliebige Basis \(B=\left\{ \overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\right\}\) des \(\mathbb{R}^{3}\) dazu. Als Basis wählt man aus praktischen Gründen die kanonische Basis \(B=\left\{ \overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}}\right\}\), die auch Standardbasis heißt. Für die Standardbasis gilt:

\[\begin{split}\left\{\begin{pmatrix}1\\ 0\\ 0 \end{pmatrix},\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix},\begin{pmatrix}0\\ 0\\ 1 \end{pmatrix}\right\}\text{ .}\end{split}\]

Die Vektoren \(\overrightarrow{e_{1}}\), \(\overrightarrow{e_{2}}\) und \(\overrightarrow{e_{3}}\) stehen paarweise senkrecht aufeinander und jeder Vektor hat die Länge \(1\). Somit legen \(\overrightarrow{e_{1}}\), \(\overrightarrow{e_{2}}\) und \(\overrightarrow{e_{3}}\) mit dem Ursprung \(O\) ein dreidimensionales kartesisches Koordinatensystem fest.

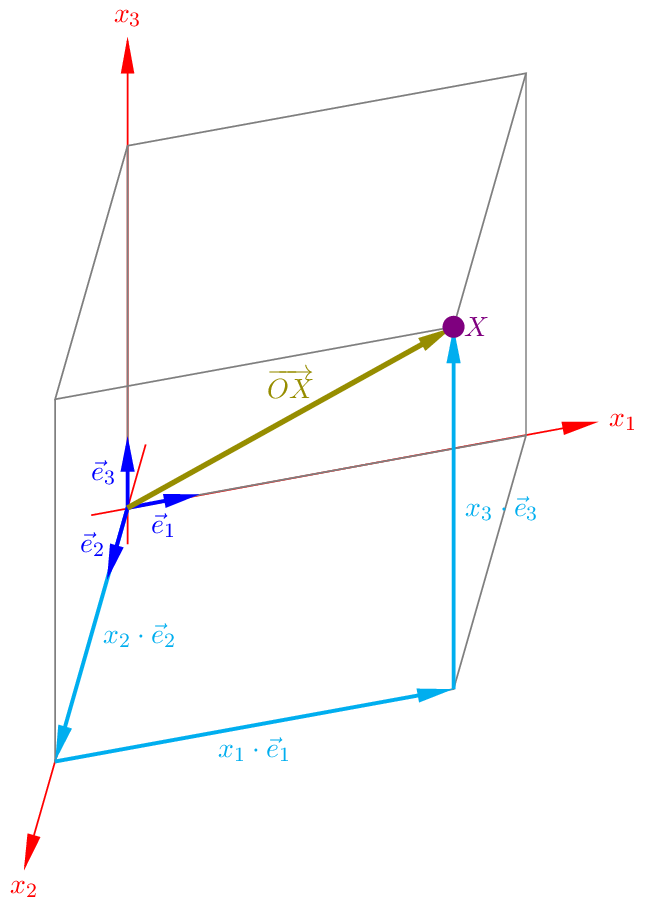
Sei nun ein beliebiger Punkt \(X\) im Anschauungsraum gegeben. Der Vektor, der den Ursprung \(O\) mit dem Punkt \(X\) verbindet, also \(\overrightarrow{OX}\) heißt Ortsvektor des Punktes \(X\).

geometrie/images/ortsvektor_x.png — Ortsvektor des Punktes X¶

Beispiel: Wir finden den Punkt \(A(5;4;3)\) mit Hilfe des Ortsvektors \(\overrightarrow{OA}=\begin{pmatrix}5\\ 4\\ 3 \end{pmatrix}\).

geometrie/images/ortsvektor_a.png — Ortsvektor des Punktes A¶

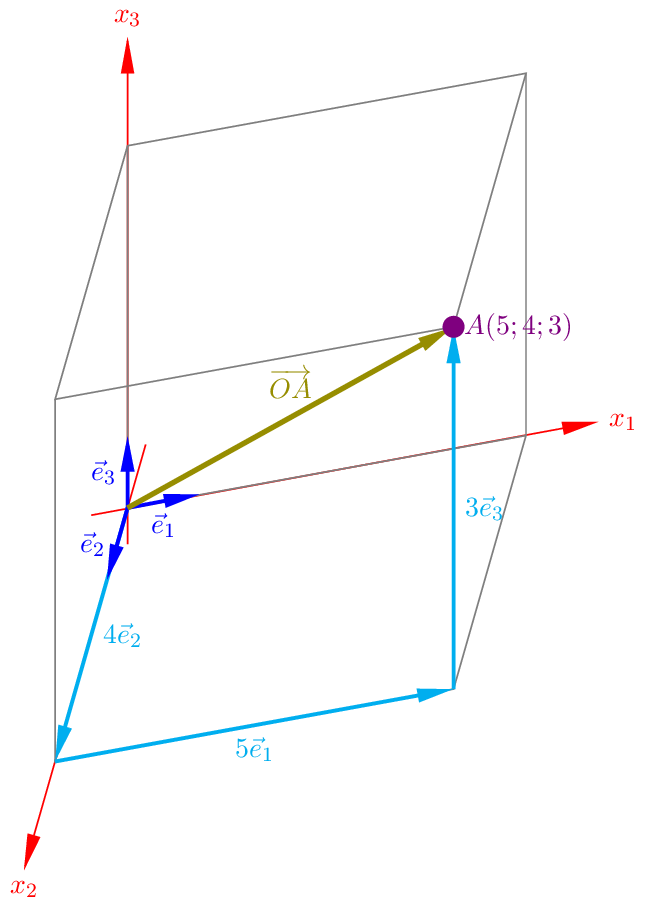
Der entsprechende Ortsvektor des Punktes A(5;4;3) ist der Vektor \(\overrightarrow{OA}\). Der Vektor \(\overrightarrow{OA}\) wird auch mit \(\overrightarrow{a}\) bezeichnet und es gilt: \(\overrightarrow{OA}=\overrightarrow{a}=\begin{pmatrix}5\\ 4\\ 3 \end{pmatrix}=5\begin{pmatrix}1\\ 0\\ 0 \end{pmatrix}+4\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix}+3\begin{pmatrix}0\\ 0\\ 1 \end{pmatrix}\).

Allgemein gilt für einen beliebigen Punkt \(X(x_{1},x_{2},x_{3})\) des Anschauungsraums:

\[\begin{split}\overrightarrow{OX}=\overrightarrow{x}=\begin{pmatrix}x_{1}\\ x_{2}\\ x_{3} \end{pmatrix}=x_{1}\begin{pmatrix}1\\ 0\\ 0 \end{pmatrix}+x_{2}\begin{pmatrix}0\\ 1\\ 0 \end{pmatrix}+x_{3}\begin{pmatrix}0\\ 0\\ 1 \end{pmatrix}\text{ .}\end{split}\]

Die Koordinaten des Punktes \(X\) im Anschauungsraum und die Koordinaten des Ortsvektors \(\overrightarrow{OX}=\overrightarrow{x}\) im Vektorraum \(\mathbb{R}^{3}\) sind \(x_{1}\), \(x_{2}\) und \(x_{3}\).

Für zwei Vektoren \(\overrightarrow{a},\overrightarrow{b}\in\mathbb{R}^{3}\) gilt bezüglich der Addition und Subtraktion von Vektoren im \(\mathbb{R}^{3}\):

\[\begin{split}\overrightarrow{a}\pm\overrightarrow{b}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}\pm\begin{pmatrix}b_{1}\\ b_{2}\\ b_{3} \end{pmatrix}=\begin{pmatrix}a_{1}\pm b_{1}\\ a_{2}\pm b_{2}\\ a_{3}\pm b_{3} \end{pmatrix}\text{ .}\end{split}\]

Zwei Vektoren \(\overrightarrow{a},\overrightarrow{b}\in\mathbb{R}^{3}\) sind genau dann gleich, falls alle Koordinaten der beiden Vektoren gleich sind: \(\overrightarrow{a}=\overrightarrow{b}\), falls \(a_{1}=b_{1}\) und \(a_{2}=b_{2}\) und \(a_{3}=b_{3}\).

Für einen Vektor \(\overrightarrow{a}\in\mathbb{R}^{3}\) und einem Skalar \(\lambda\in\mathbb{R}\) gilt bezüglich der Multiplikation eines Vektors mit einem Skalar:

\[\begin{split}\lambda\cdot\overrightarrow{a}=\lambda\cdot\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}=\begin{pmatrix}\lambda\cdot a_{1}\\ \lambda\cdot a_{2}\\ \lambda\cdot a_{3} \end{pmatrix}\text{ .}\end{split}\]