Geometrische Anwendungen

• Aufgaben

In der analytischen Geometrie werden die Ergebnisse der Vektoralgebra zur rechnerischen Lösung geometrischer Probleme benutzt. In einem dreidimensionalen kartesischen Koordinatensystem hat jeder Punkt \(X\), einen entsprechenden Ortsvektor \(\overrightarrow{OX}\). Eine weitere Aufgabe besteht nun darin, die Gebilde Gerade und Ebene mit Hilfe von Vektorgleichungen darzustellen.

Die Gerade

Eine Gerade \(g\) ist festgelegt durch einen Punkt \(A\in g\) und einem Vektor \(\vec{u}\) . Der Punkt \(A\) heißt Aufpunkt oder Stützpunkt von \(g\). Der Vektor \(\vec{u}\) ist der Richtungsvektor von \(g\). Den Ortsvektor \(\vec{x}=\overrightarrow{OX}\) eines beliebigen Punktes \(X\) von \(g\) können wir nun mit einer Geradengleichung in Parameterform darstellen.

Allgemein gilt:

Im \(\mathbb{R}^{2}\) oder \(\mathbb{R}^{3}\) werden Geradengleichungen in der Parameterform angegeben.

\(g:\vec{x}=\overrightarrow{OA}+\lambda\vec{u}\) , oder

\(g:\begin{pmatrix}x_{1}\\ x_{2}\\ x_{3} \end{pmatrix}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}+\lambda\begin{pmatrix}u_{1}\\ u_{2}\\ u_{3} \end{pmatrix}\) mit \(\lambda\in\mathbb{R}\)

---

Durchläuft \(\lambda\) alle reellen Zahlen, so beschreibt \(\vec{x}\) alle Punkte der Geraden \(g\). Der Skalar \(\lambda\) heißt Parameter der Geradengleichung von \(g\). Jedem Punkt \(X\) der Geraden \(g\) ist eindeutig ein bestimmter \(\lambda\)-Wert zugeordnet. Umgekehrt entspricht jedem Wert \(\lambda\in\mathbb{R}\) genau ein Punkt \(X\in g\).

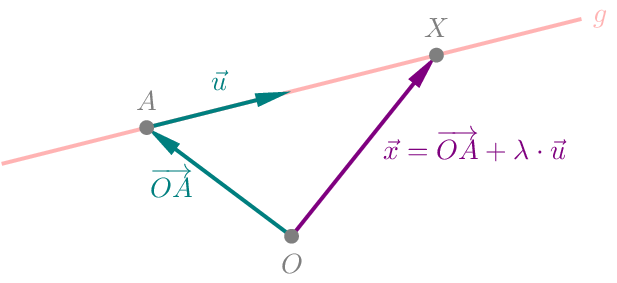
Um zu untersuchen, ob ein Punkt \(B(b_{1};b_{2};b_{3})\) auf \(g\) liegt, setzt man \(B\) in \(g\) ein und erhält eine Vektorgleichung.

\(\begin{pmatrix}b_{1}\\ b_{2}\\ b_{3} \end{pmatrix}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}+\lambda\begin{pmatrix}u_{1}\\ u_{2}\\ u_{3} \end{pmatrix}\)

Falls die Vektorgleichung eine eindeutige Lösung hat, liegt der Punkt \(B\) auf der Geraden \(g\), kurz \(B\in g\). Ansonsten liegt der Punkt \(B\) nicht auf der Geraden \(g\).

---

Allgemein gilt:

Für die gegenseitige Lage zweier Geraden \(g\) und \(h\) gibt es folgende Möglichkeiten:

• \(g\) und \(h\) sind identisch,

• \(g\) und \(h\) sind echt parallel,

• \(g\) und \(h\) schneiden sich in genau einem Punkt,

• \(g\) und \(h\) sind windschief (nur im \(\mathbb{R}^{3}\) möglich).

Die gegenseitige Lage von \(g\) und \(h\) bestimmten wir mit Hilfe ihrer Parametergleichungen.

\(g:\vec{x}=\vec{a}+\lambda \vec{u}\) ; \(\lambda \in \mathbb{R}\)

\(h:\vec{x}=\vec{b}+\mu \vec{v}\) ; \(\mu \in \mathbb{R}\)

Bei der Untersuchung der Lage zweier Geraden \(g\) und \(h\) spielen die Richutngsvektoren der beiden Geraden eine zentrale Rolle.

• Sind die Richtungsvektoren \(\vec{u}\) und \(\vec{v}\) parallel, so sind die Geraden \(g\) und \(h\) identisch, falls der Aufpunkt \(A\) von \(g\) auf \(h\) liegt. Ansonsten sind die beiden geraden echt parallel.

• Sind die Richtungsvektoren \(\vec{u}\) und \(\vec{v}\) nicht parallel, so berechnen wir den Wert \(v=\left(\vec{u}\times\vec{v}\right)\cdot\overrightarrow{AB}.\) Ist \(v=0\), so schneiden sich \(g\) und \(h\) in genau einem Punkt \(S\). In diesem Fall liegen \(\vec{u},\vec{v},\overrightarrow{AB}\) in einer Ebene. Ist \(v\neq 0\) , so sind die Geraden \(g\) und \(h\) windschief.

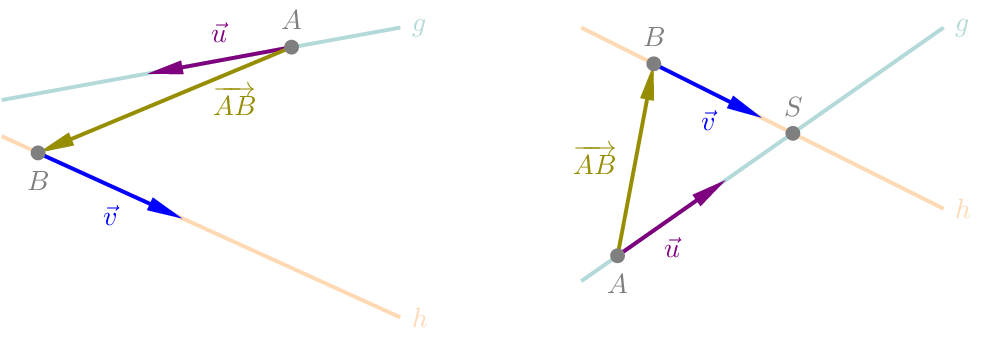
Zwei sich schneidende Geraden \(g\) und \(h\) haben den Punkt \(S\) gemeinsam und schließen zwei Winkel ein, die sich zu \(180^{\circ}\) ergänzen. Die Koordinaten des Punktes \(S\) werden durch Gleichsetzten der Parametergleichung von \(g\) und \(h\) berechnet. Den Schnittwinkel \(\varphi\) der Geraden \(g\) und \(h\) berechnen wir mit der Formel zur Berechnung eines Winkels. Mit dem Betrag im Zähler sorgen wir dafür, dass wir einen spitzen Winkel erhalten.

Allgemein gilt:

Bei der Berechnung des Winkels \(\varphi\), den zwei Geraden einschließen, die sich in einem Punkt schneiden, steht das Skalarprodukt im Betrag.

\(\varphi =\arccos \dfrac{\left\vert \vec{u}\cdot \vec{v}\right\vert }{\left\vert \vec{u}\right\vert \cdot \left\vert \vec{v}\right\vert}\) ; \(0^{\circ} \leq \varphi \leq 90^{\circ}\)

Die Ebene

Die Lage einer Ebene \(E\) im \(\mathbb{R}^{3}\) ist festgelegt durch einen Stützpunkt \(A\) und durch zwei nicht parallele Richtungsvektoren \(\vec{u}\neq \vec{0}\) und \(\vec{v}\neq \overrightarrow{0}\).

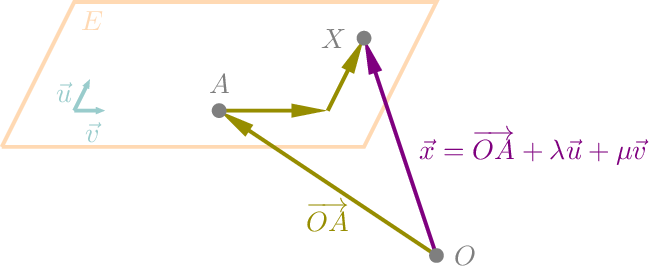
Den Ortsvektor \(\vec{x}=\overrightarrow{OX}\) eines beliebigen Punktes \(X\) von \(E\) können wir nun mit einer Ebenengleichung in Parameterform darstellen.

Allgemein gilt:

Im \(\mathbb{R}^{3}\) werden Ebenengleichungen in der Parameterform angegeben.

\(E:\vec{x}=\overrightarrow{OA}+\lambda\vec{u}+\mu\vec{v}\) , oder

\(E:\begin{pmatrix}x_{1}\\ x_{2}\\ x_{3} \end{pmatrix}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}+\lambda\begin{pmatrix}u_{1}\\ u_{2}\\ u_{3} \end{pmatrix}+\mu\begin{pmatrix}v_{1}\\ v_{2}\\ v_{3} \end{pmatrix}\) mit \(\lambda,\mu\in\mathbb{R}\)

Der Punkt \(A\) heißt Aufpunkt oder Stützpunkt von \(E\). Die beiden Vektoren \(\vec{u}\) und \(\vec{v}\) sind die Richtungsvektoren von \(E\).

---

Durchlaufen \(\lambda\) und \(\mu\) alle reellen Zahlen, so beschreibt \(\vec{x}\) alle Punkte der Ebene \(E\). Die Skalare \(\lambda\) und \(\mu\) heißen Parameter der Ebenengleichung von \(E\).

---

Jedem Punkt \(X\) der Ebene \(E\) ist eindeutig ein bestimmter \(\lambda\)-Wert und \(\mu\)-Wert zugeordnet. Umgekehrt entspricht jedem Wertepaar \(\left( \lambda ,\mu \right)\) genau ein Punkt \(X\in E\). Daraus ergibt sich, dass ein Punkt \(B(b_{1};b_{2};b_{3})\) genau dann auf der Ebene \(E\) liegt, wenn die Komponenten seines Ortsvektors \(\vec{b}\) beim Einsetzten in die Punkt-Richtungs-Gleichung der Ebene \(E\) stets dieselben Werte für \(\lambda\) und \(\mu\) ergeben.

---

Die Lage einer Ebene \(E\) lässt sich auch durch drei verschiedene Punkte \(A\), \(B\) und \(C\) bestimmen. Als Richtungsvektoren der Ebene \(E\) nehmen wir beispielsweise die Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\).

---

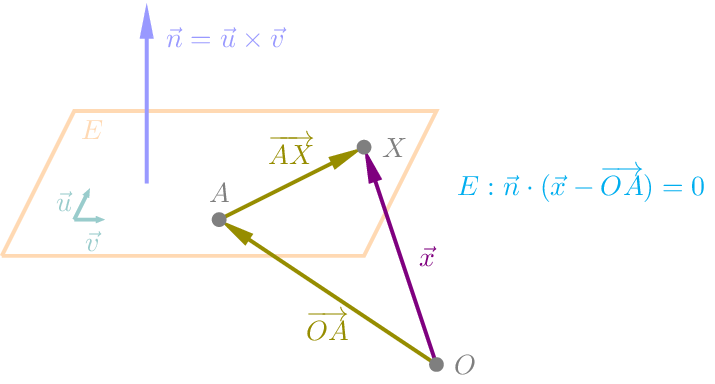
Im \(\mathbb{R}^{3}\) haben wir die Möglichkeit eine Ebene \(E\) auch anders darzustellen. Wir wissen, dass es zu zwei linear unabhängigen und vom Nullvektor verschiedenen Vektoren \(\vec{u}\) und \(\vec{v}\) unendlich viele senkrechte Vektoren unterschiedlicher Länge gibt, die alle die gleiche oder die entgegengesetzte Richtung haben. Diese Vektoren sind ein Vielfaches des Vektors, den wir mit dem Kreuzprodukt aus \(\vec{u}\) und \(\vec{v}\) berechnen.

\(\rho(\vec{u}\times\vec{v})\bot\vec{u}\) und \(\rho(\vec{u}\times\vec{v})\bot\vec{v}\) mit \(\rho\in\mathbb{R}\)

Ein zu den Richtungsvektoren \(\vec{u}\) und \(\vec{v}\) einer Ebene \(E\) senkrechter Vektor \(\vec{n}\) heißt Normalenvektor der Ebene \(E\). Im \(\mathbb{R}^{3}\) finden wir einen Normalenvektor \(\vec{n}\) mit Hilfe des Vektorprodukts \(\vec{n}=\vec{u}\times\vec{v}\).

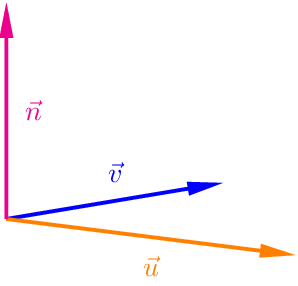
Nehmen wir den Aufpunkt \(A\) und einen beliebigen anderen Punkt \(X\) von \(E\), so erkennen wir, dass \(\vec{n}\bot\overrightarrow{AX}\) und folgern daraus \(\vec{n}\cdot\overrightarrow{AX}=0\). Das gilt für alle Punkte der Ebene \(E\) und für keine anderen. Nach diesem Prinzip stellen wir eine Gleichung der Ebene \(E\) auf. Diese parameterfreie Gleichung der Ebene \(E\) heißt Normalenform der Ebene \(E\). Die ausmultiplizierte Normalenform nennen wir Koordinatenform der Ebene \(E\) im \(\mathbb{R}^{3}\).

Allgemein gilt:

Im \(\mathbb{R}^{3}\) werden Ebenengleichungen in der Normalenform und der Koordinatenform angegeben.

\(\vec{n}=\vec{u}\times\vec{v}\) (Normalenvektor von \(E\) )

\(E:\vec{n}\cdot(\vec{x}-\overrightarrow{OA})=0\) (Normalenform von \(E\) )

\(E:n_{1}x_{1}+n_{2}x_{2}+n_{3}x_{3}+d=0\) (Koordinatenform von \(E\) )

Lage einer Geraden zu einer Ebene

Die gegenseitige Lage einer Geraden \(g\) zu einer Ebene \(E\) untersuchen wir am einfachsten, wenn eine Normalengleichung der Ebene \(E\) vorliegt. Hat eine Ebene mit den Achsen des Koordinatensystems gemeinsame Punkte, so nennen wir diese Punkte Spurpunkte von \(E\).

\(g:\vec{x}=\overrightarrow{OA}+\lambda\vec{u}\)

\(E:\vec{n}(\vec{x}-\overrightarrow{OB})=0\)

Allgemein gilt:

Für die gegenseitige Lage einer Geraden \(g\) zu einer Ebene \(E\) im \(\mathbb{R}^{3}\) gibt es folgende Möglichkeiten:

• \(g\) liegt in \(E\),

• \(g\) und \(E\) sind echt parallel, oder

• \(g\) schneidet \(E\) in genau einem Punkt.

Bei der Untersuchung der Lage von \(g\) zu \(E\) setzen wir die Parametergleichung von \(g\) in die Normalengleichung von \(E\) ein. Wir erhalten dadurch eine lineare Gleichung mit der Unbekannten \(\lambda\).

\(\vec{n}(\overrightarrow{OA}+\lambda\vec{u}-\overrightarrow{OB})=0\)

Wenn wir eine lineare Gleichung lösen, so treten dabei drei unterschiedliche Fälle auf.

• Ist die Gleichung eindeutig lösbar mit der Lösung \(\lambda _{S}\), so schneidet die Gerade \(g\) die Ebene \(E\) in genau einem Punkt \(S\). Setzen wir nun den Wert von \(\lambda _{S}\) in \(g\) ein, so erhalten wir den Ortsvektor \(\overrightarrow{OS}\) des Schnittpunktes \(S\).

• Hat die Gleichung keine reelle Lösung, so sind die Gerade \(g\) und die Ebene \(E\) echt parallel.

• Hat die Gleichung unendlich viele Lösungen, so liegt die Gerade \(g\) in der Ebene \(E\).

---

Schneidet eine Gerade \(g\) eine Ebene \(E\) in genau einen Punkt \(S\), so entsteht der Schnittwinkel \(\varphi=\measuredangle (g;E)\). Den Winkel \(\varphi\) berechnen wir mit der Formel zur Berechnung eines Winkels. Mit dem Betrag im Zähler sorgen wir dafür, dass wir einen spitzen Winkel erhalten.

Allgemein gilt:

Bei der Berechnung des Winkels \(\varphi\), den eine Gerade und eine Ebene einschließen, die sich in einem Punkt schneiden, steht das Skalarprodukt im Betrag.

\(\varphi =90^{\circ}-\arccos \dfrac{\left\vert \vec{u}\cdot \vec{n}\right\vert }{\left\vert \vec{u}\right\vert \cdot \left\vert \vec{n}\right\vert}\) ; \(0^{\circ} \leq \varphi \leq 90^{\circ}\)

Der Vektor \(\vec{n}\) ist ein Normalenvektor der Ebene \(E\).

Gegenseitige Lage zweier Ebenen

Die gegenseitige Lage zweier Ebenen \(E\) und \(F\) untersuchen wir am einfachsten, wenn beide Ebenen in einer Normalengleichung vorliegen. Die Spurgeraden einer Ebene \(E\) sind die Schnittgeraden der Ebene \(E\) mit dem Koordinatenebenen.

\(E:\vec{n}_{E}(\vec{x}-\overrightarrow{OA})=0\)

\(F:\vec{n}_{F}(\vec{x}-\overrightarrow{OB})=0\)

Allgemein gilt:

Für die gegenseitige Lage zweier Ebenen \(E\) und \(F\) im \(\mathbb{R}^{3}\) gibt es folgende Möglichkeiten:

• \(E\) und \(F\) sind identisch,

• \(E\) und \(F\) sind echt parallel, oder

• \(E\) und \(F\) schneiden sich in einer Geraden.

Bei der Untersuchung der Lage von \(E\) zu \(F\) spielen die Normalenvektoren \(\vec{n}_{E}\) und \(\vec{n}_{F}\) eine wichtige Rolle.

• Sind die Normalenvektoren \(\vec{n}_{E}\) und \(\vec{n}_{F}\) linear abhängig, so sind \(E\) und \(F\) parallel. Liegt der Aufpunkt \(A\) von \(E\) auf \(F\), so sind die beiden Ebenen identisch. Ansonsten sind die beiden Ebenen echt parallel.

• Sind die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{F}\) linear unabhängig, so haben die Ebenen \(E\) und \(F\) eine gemeinsame Schnittgerade \(s\).

\(s:\vec{x}=\overrightarrow{OQ}+\tau\vec{w}\)

Der Richtungsvektor \(\vec{w}\) ist parallel zu dem Vektor \(\vec{n}_{E}\times\vec{n}_{F}\) und die Koordinaten des Punktes \(Q\) sind eine Lösung des Gleichungssystems, das die Koordiantenform der Ebenen \(E\) und \(F\) bestimmen.

---

Zwei sich schneidende Ebenen \(E\) und \(F\) schließen zwei Winkel ein, die sich zu \(180^{\circ}\) ergänzen. Der Schnittwinkel \(\varphi=\measuredangle(E;F)\) der Ebenen \(E\) und \(F\) ist der kleinere dieser Winkel.

\[\varphi =\measuredangle \left( E;F\right) \text{ mit }0^{\circ} \leq \varphi \leq 90^{\circ} \text{.}\]

Allgemein gilt:

Der Schnittwinkel \(\varphi\) zweier sich schneidenden Ebenen \(E\) und \(F\) entspricht dem spitzen Winkel, den die Normalenvektoren \(\vec{n}_{E}\) und \(\vec{n}_{F}\) bestimmen.

\(\varphi =\arccos \dfrac{\left\vert \vec{n}_{E}\cdot \vec{n}_{F}\right\vert }{\left\vert \vec{n}_{E}\right\vert \cdot \left\vert \vec{n}_{F}\right\vert}\) ; \(0^{\circ}\leq\varphi\leq 90^{\circ}\)