Kraft als vektorielle Größe¶
Kraft als vektorielle Größe¶
Aus täglicher Erfahrung und aus der Physik wissen wir, was eine Kraft ist. Kräfte erkennt man an ihrer Wirkungen und sie sind die Ursache für
Bewegungsänderungen und
Formänderungen
von Körpern. Diese Fähigkeiten der Kräfte macht man sich zu Nutze, um die Kräfte zu messen. Dazu zählt die Messung der Beschleunigung eines Fahrzeugs, oder sie Messung der Gewichtskraft eines Körpers mit der Federwaage.
Die Kraft wird meistens mit den Formelbuchstaben \(\vec{F}\) und in \(\mathrm{N}\) (Newton) gemessen. Dabei gilt:
\(1\,\mathrm{N}=1\dfrac{kg\cdot m}{s^{2}}\).
Da Newton eine kleine Einheit für die in der Technik auftretenden Kräfte ist, werden wir häufig die Einheit \(\mathrm{kN}\) oder \(\mathrm{MN}\) antreffen. Hier gilt:
\(1\,\mathrm{kN}=10^{3}\,\mathrm{N}\) und \(1\,\mathrm{MN}=10^{6}\,\mathrm{N}\).
Wird eine Kraft beispielsweise mit \(F=25\,\mathrm{kN}\) angegeben, so ist diese Kraft nicht vollständig charakterisiert. Der Zahlenwert \(25\) ist der Betrag der Kraft und und die Einheit ist hier \(\mathrm{kN}\). Dazu kommen noch Angriffspunkt, Richtung und Richtungssinn des Kraftvektors \(\vec{F}\).
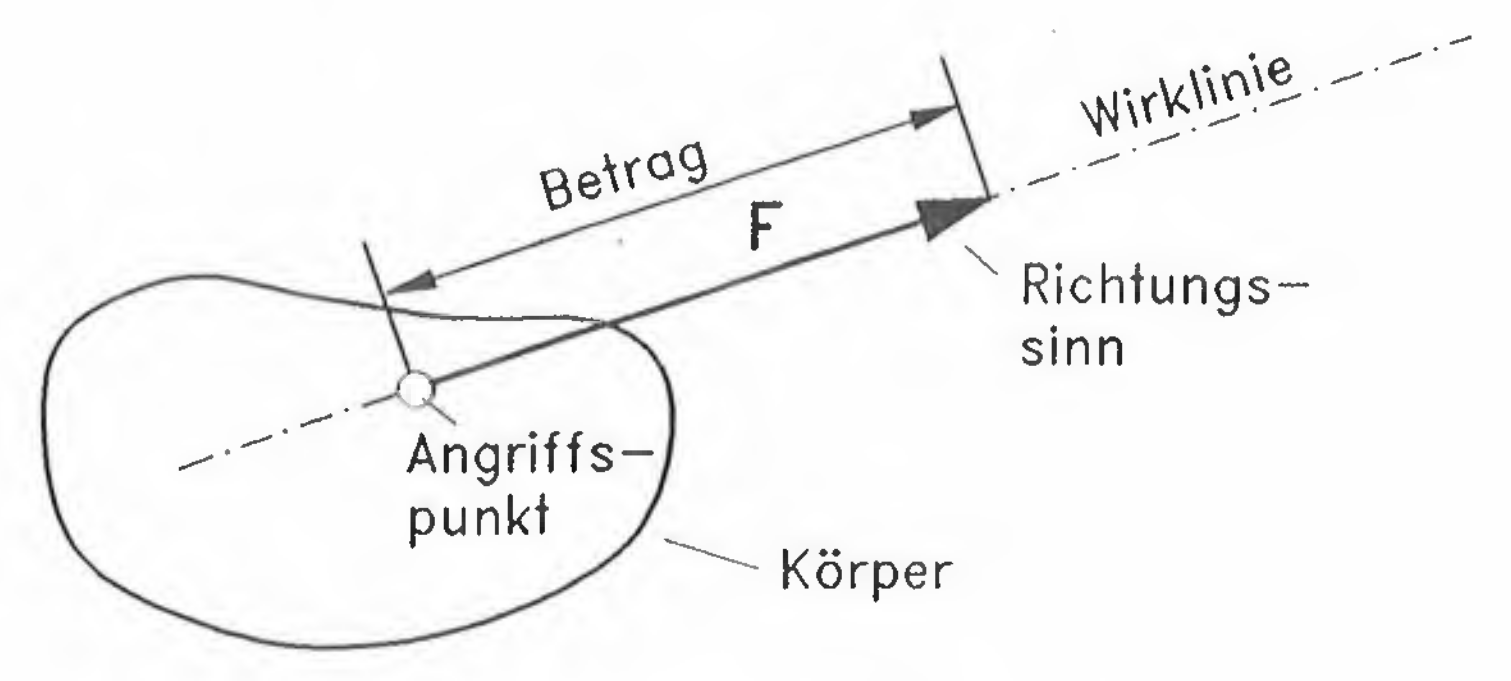
Die durch Angriffspunkt und Richtung der Kraft festgelegte Gerade heißt Wirklinie oder Wirkungslinie der Kraft \(\vec{F}\). Damit ist die Kraft eine vektorielle, also eine gerichtete physikalische Größe. Dafür wird die Bezeichnung \(\vec{F}\) verwendet. Wenn nur der Betrag der Kraft gemeint ist, so schreiben wir einfach \(F\). Es gilt also:
\(|\vec{F}|=F\).
Die Beschreibung eine realen Kraft durch einen Vektor ist eine Idealisierung. Kräfte greifen in Wirklichkeit nicht punktförmig sondern flächenhaft an einem Körper an. Die Gewichtskraft wirkt sogar auf das ganze Volumen eines Körpers. Man kann sich vorstellen, dass die auf eine Fläche oder Volumen verteilte Einzelkräfte zu einer resultierenden Kraft zusammengefasst werden, die den Kraftvektor repräsentiert. Der Angriffspunkt dieses Kraftvektors ist dann beispielsweise bei der Gewichtskraft der Schwerpunkt des Körpers.
Die Berechnungen zu Kräften bauen auf einige Grundaussagen der Physik auf. Diese gelten aber nur dann, wenn man davon ausgeht, dass sich ein Körper unter dem Einfluss eine Kraft nicht verformt. In Wirklichkeit ist das nicht so, aber die Verformung ist so gering, dass die Berechnungen zu gut brauchbaren Ergebnissen führen.
Eine Kraft \(\vec{F}\) heißt Nullkraft, wenn für den Betrag der Kraft gilt: \(F=0\,\mathrm{N}\). Man schreibt dazu auch: \(\vec{F}=\vec{0}\).
Eine Kraft \(\vec{F}\) kann entlang ihrer Wirkungslinie verschoben werden. Die Wirkung der Karft auf einen Körper ändert sich dabei nicht.
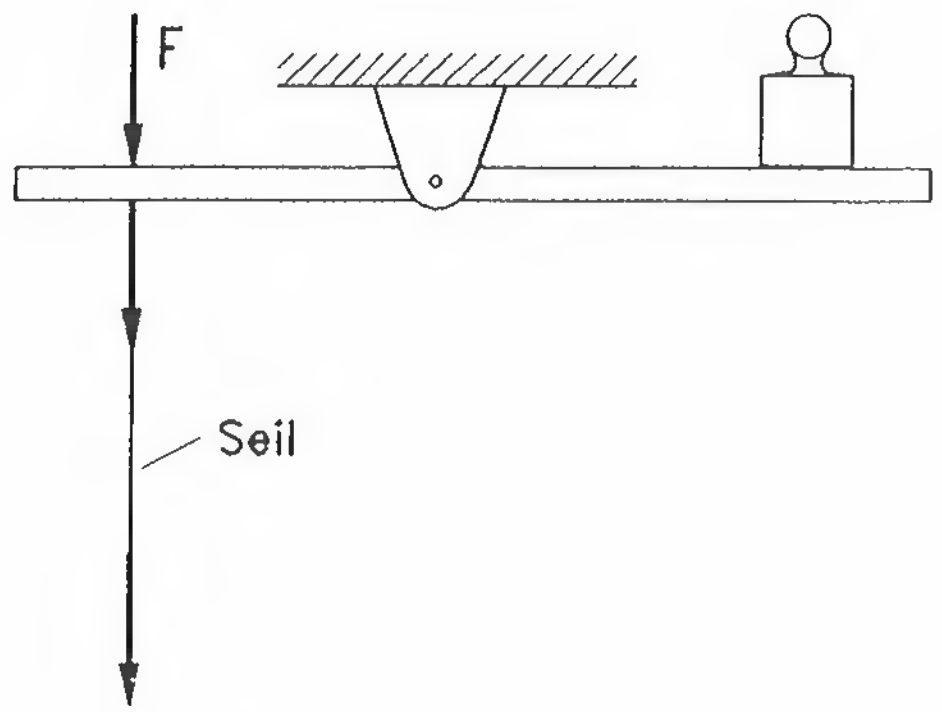
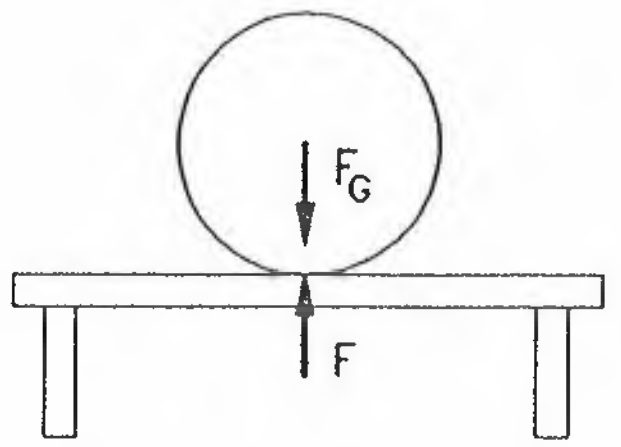
Zu jeder auf einen Körper wirkenden Kraft existiert immer eine auf einen anderen Körper wirkende Gegenkraft. Dabei sind Kraft und Gegenkraft gleich groß, besitzen dieselbe Wirkungslinie und sind entgegengesetzt gerichtet.
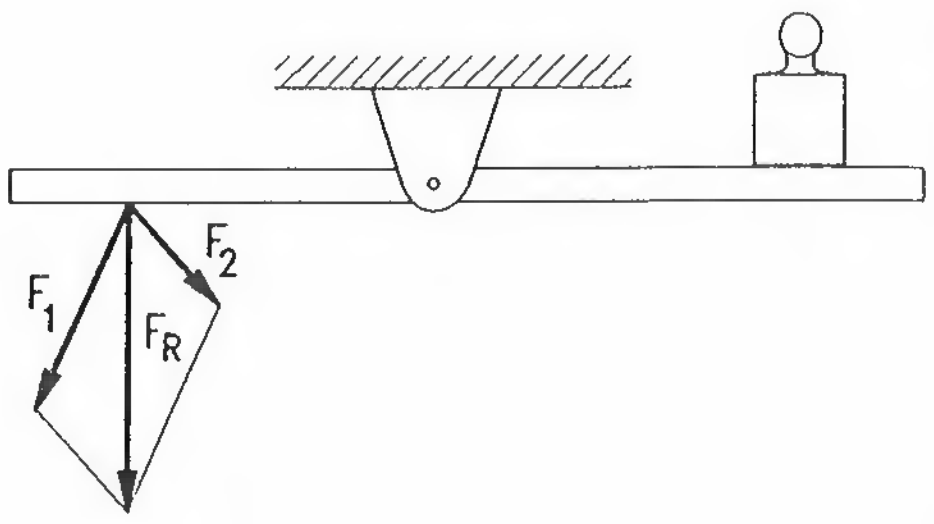
Zwei an einen Punkt angreifenden Kräfte können zu einer resultierenden Kraft oder Ersatzkraft zusammengefasst werden, indem man die Diagonale des von den beiden Kraftvektoren gebildeten Parallelogramms bildet. Hier gilt: \(\vec{F}_{R}=\vec{F}_{1}+\vec{F}_{2}\). Das Gleiche Ergebnis erhält man wenn die Kräfte mit Hilfe einer Vektorkette addiert werden.
Im folgenden Beispiel wird ein Körper von fünf Kräften belastet und die Wirkungslinien der fünf Kräfte schneiden sich alle im Punkt \(Q\).
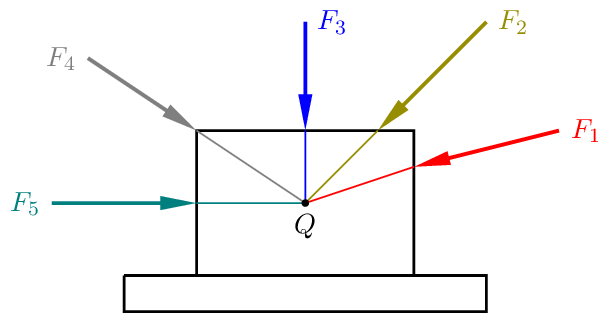
Die Ersatzkraft \(F_{R}\) der fünf Kräfte bestimmen wir mit Hilfe einer Vektorkette.
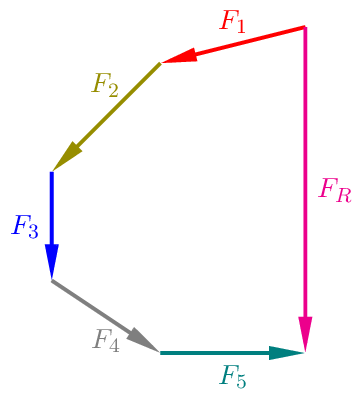
Wichtig
Beim Lösen von Aufgaben ist es wichtig, dass der Unterschied zwischen Ersatzkraft (resultierende Kraft) und Gegenkraft klar ist.