Vektorielle Räume¶
Bei der Beschreibung und Berechnung physikalischer Sachverhalte mit Hilfe von physikalischen Größen kommt es häufig nicht nur auf die Größe des Messwertes an, sondern auch auf die Richtung in der die physikalische Größe wirkt. Die Kraft, die Geschwindigkeit oder der Impuls sind solche physikalische Größen. Beim Segeln oder Windsurfen weiß man, dass nicht nur die Windstärke, sondern auch die Windrichtung eine wichtige Rolle spielen. Dabei ist in einem mehr oder weniger großen Gebiet der Wind nach Stärke und Richtung konstant. Dies kann man durch eine gemeinsame Größe und mit Hilfe eines Vektors ausdrücken.
Zunächst soll geklärt werden, was in der Zeichenebene, also im zweidimensionalen Raum und im geometrischen Anschauungsraum, also im dreidimensionalen Raum unter einem Vektor zu verstehen ist. Die Zeichenebene wird im Folgenden kurz \(\mathbb{R}^{2}\) und der geometrische Anschauungsraum mit \(\mathbb{R}^{3}\) bezeichnet.
Im \(\mathbb{R}^{2}\) oder \(\mathbb{R}^{3}\) versteht man unter einem Vektor \(\vec{a}\) die Menge aller gerichteten Strecken mit gleicher Länge und gleicher Richtung. Jede gerichtete Strecke aus dieser Menge heißt Repräsentant des Vektors.
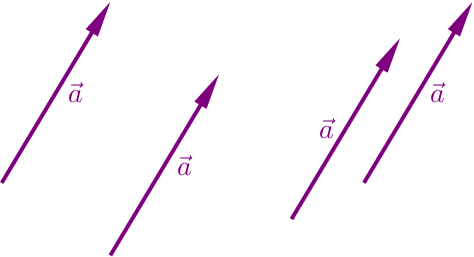
Parallelgleiche Vektoren
Ein Vektor lässt sich auch als Translation deuten. Eine Abbildung durch Translation (Parallelverschiebung) im \(\mathbb{R}^{2}\) oder im \(\mathbb{R}^{3}\), bei der jedem Punkt \(P\) eindeutig ein Punkt \(P^{\prime}\) zugeordnet wird, ist eindeutig bestimmt durch die Angabe eines einzigen Verschiebungspfeils. Ist ein solcher Verschiebungspfeil \(\overrightarrow{PP^{\prime }}\) gegeben, so wird bei dieser Translation jeder weitere Punkt \(A\) so auf einen Punkt \(A^{\prime }\) abgebildet, dass die Pfeile \(\overrightarrow{AA^{\prime }}\) und \(\overrightarrow{PP^{\prime }}\) zueinander parallel, gleichorientiert und gleich lang sind. Verschiedene Pfeile, die zueinander parallel, gleichorientiert und gleich lang sind nennen wir kurz parallelgleich.
Unter dem Nullvektor \(\vec{0}\) verstehen wir den Vektor, dessen Repräsentanten die Länge \(0\) haben. Unter dem Gegenvektor \(-\vec{b}\) zu einem Vektor \(\vec{b}\) versteht man den Vektor, dessen Repräsentanten parallel zu denen von \(\vec{b}\), die gleiche Länge wie die von \(\vec{b}\) haben, aber entgegengesetzt orientiert zu denen von \(\vec{b}\) sind.
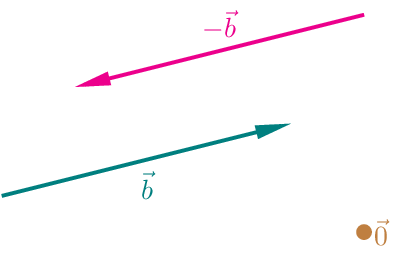
Gegenvektor und Nullvektor
Wählen wir \(\vec{a}\) und \(\vec{b}\) zwei geometrische Vektoren aus dem \(\mathbb{R}^{2}\) oder dem \(\mathbb{R}^{3}\), so versteht man aus der Summe \(\vec{a}+\overrightarrow{b}\) dieser Vektoren denjenigen Vektor, dessen Repräsentant man nach folgender Vorschrift erhält: Man setzt an der Spitze eines Repräsentanten von \(\vec{a}\) einen Repräsentanten von \(\vec{b}\) mit dessen Fuß an. Der Pfeil vom Fuß des Repräsentanten von \(\vec{a}\) zur Spitze des Repräsentanten von \(\vec{b}\) ist dann ein Repräsentant von \(\vec{a}+\vec{b}\).
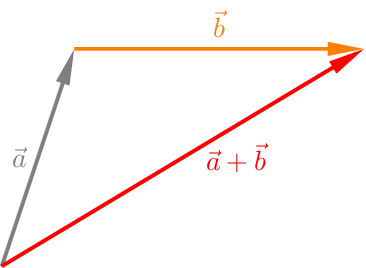
Addition zweier Vektoren
Für alle Vektoren aus dem \(\mathbb{R}^{2}\) oder dem \(\mathbb{R}^{3}\) gelten folgende Rechengesetze:
\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
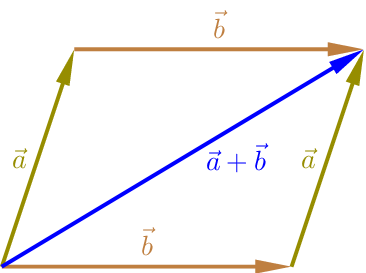
Kommutativgesetz
\(( \vec{a}+\vec{b}) +\vec{c}=\vec{a}+( \vec{b}+\vec{c})\)
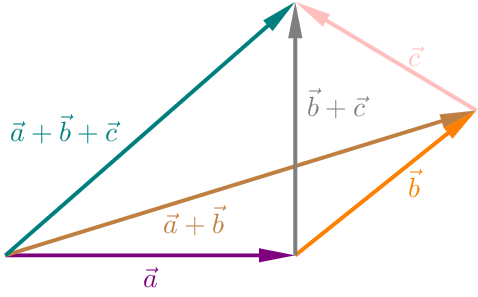
Assoziativgesetz
\(\vec{a}+( -\vec{a}) =\vec{a}-\vec{a}=\vec{0}\)
\(\vec{a}-\vec{b}=\vec{a}+( -\vec{b})\) (Subtraktion von Vektoren)
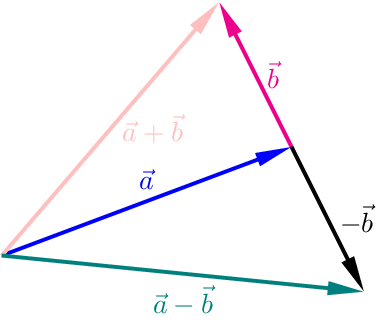
Subtraktion zweier Vektoren
Multiplikation eines Vektors mit einer reellen Zahl: Ist \(\lambda \in \mathbb{R}\) ein Skalar, also eine beliebige reelle Zahl und \(\vec{a}\) ein geometrischer Vektor aus dem \(\mathbb{R}^{2}\) oder \(\mathbb{R}^{3}\), so versteht man unter dem Produkt \(\lambda \cdot \vec{a}\) den geometrischen Vektor, dessen Repräsentanten
parallel zu den Repräsentanten von \(\vec{a}\) sind,
die \(\left\vert \lambda \right\vert\)-fache Länge wie die Repräsentanten von \(\vec{a}\) haben und
für \(\lambda >0\) die gleiche Orientierung wie \(\vec{a}\) oder
für \(\lambda <0\) die entgegengesetzte Orientierung wie \(\vec{a}\) haben.
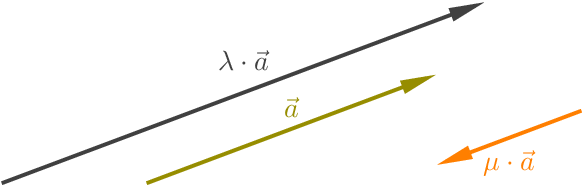
S-Multiplikation