Aufgaben

Aufgabe 1

Lösen Sie folgende Vektorgleichungen nach \(\vec{x}\) auf.

1. \(2(3\vec{a}-3\vec{b}+\vec{x})-\frac{1}{2}(3\vec{a}-3\vec{b}-12\vec{c})+4\vec{x}=\vec{0}\)

2. \(3(2\vec{a}-\vec{x}+3\vec{b})-\frac{1}{4}(8\vec{a}+4\vec{b}+2\vec{x})=\frac{1}{2}(-3\vec{x}-\vec{c})\)

3. \(\frac{1}{4}(-12\vec{a}-\vec{c}+4\vec{x})-\frac{1}{2}(3\vec{b}+4\vec{c}+6\vec{x})=2\vec{x}-5\vec{a}-\vec{c}\)

4. \(\frac{3}{2}\vec{a}+\vec{x}-\frac{1}{8}(2\vec{b}-4\vec{x})=-\frac{3}{2}\vec{x}-\frac{1}{4}\vec{a}\)

Aufgabe 2

Zeigen Sie, dass die Seiten des Mitteldreiecks parallel und halb so lang wie die Seiten des entsprechenden Dreiecks sind.

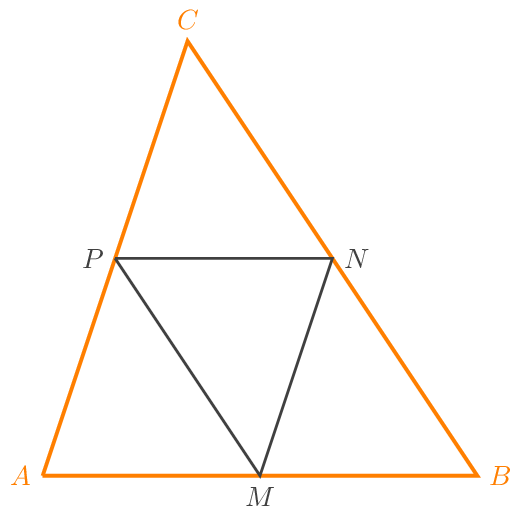
Aufgabe 3

In einem Parallelogramm \(ABCD\) teilt der Punkt \(P\) die Strecke \(\overline{AB}\) von \(A\) aus im Verhältnis \(1:2\). Der Punkt \(Q\) teilt die Strecke \(\overline{CD}\) von \(C\) aus im Verhältnis \(3:2\).

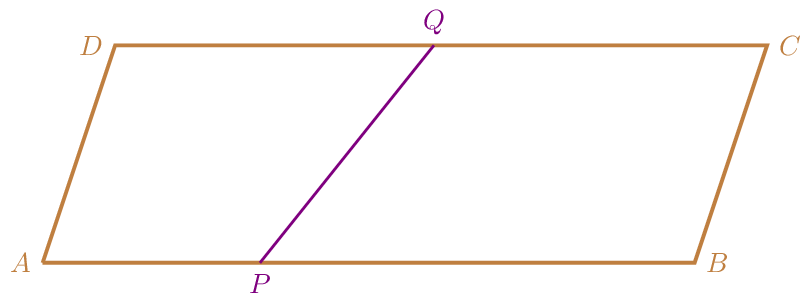
Drücken Sie den Vektor \(\overrightarrow{PQ}\) durch \(\vec{a}=\overrightarrow{AB}\) und \(\vec{b}=\overrightarrow{AD}\) aus.

Aufgabe 4

Eine Pyramide hat die Spitze \(S\) und das Parallelogramm \(ABCD\) als Grundfläche. Es gilt: \(\overrightarrow{AB}=\vec{a}\) ; \(\overrightarrow{AD}=\vec{b}\) ; \(\overrightarrow{AS}=\vec{c}\).

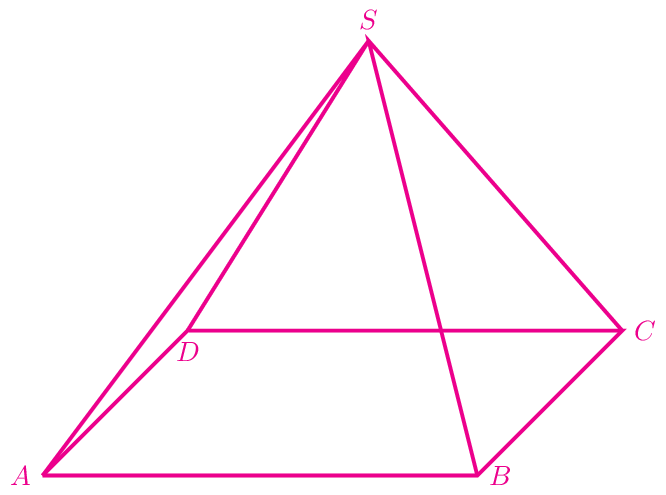
Drücken Sie die Vektoren \(\overrightarrow{BS}\), \(\overrightarrow{CS}\), \(\overrightarrow{DS}\), \(\overrightarrow{CA}\) und \(\overrightarrow{DB}\) durch \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) aus.

Aufgabe 5

Gegeben ist die Pyramide aus Aufgabe (4). \(M\) ist der Mittelpunkt der Grundfläche, \(N\) der Schwerpunkt des Dreiecks \(BCS\).

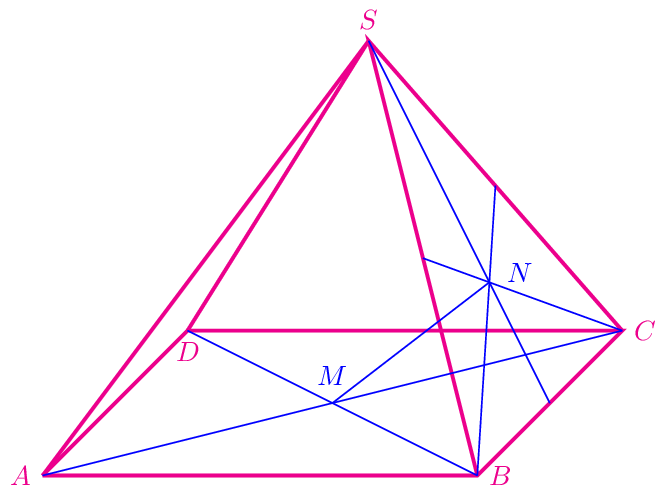
Drücken Sie \(\overrightarrow{MN}\) durch \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) aus.

Aufgabe 6

Durch die Punkte \(A\), \(B\), \(C\) und \(D\) wird eine dreiseitige Pyramide mit der Grundfläche \(ABC\) und der Spitze \(D\) festgelegt. Weiter gilt: \(\overrightarrow{AB}=\vec{a}\), \(\overrightarrow{AC}=\vec{b}\) und \(\overrightarrow{AD}=\vec{c}\). \(S\) ist der Schwerpunkt des Dreiecks \(ABC\). Der Punkt \(T\) liegt auf der Strecke \(\overline{BD}\) und teilt diese im Verhältnis \(3:2\) von Punkt \(B\) aus.

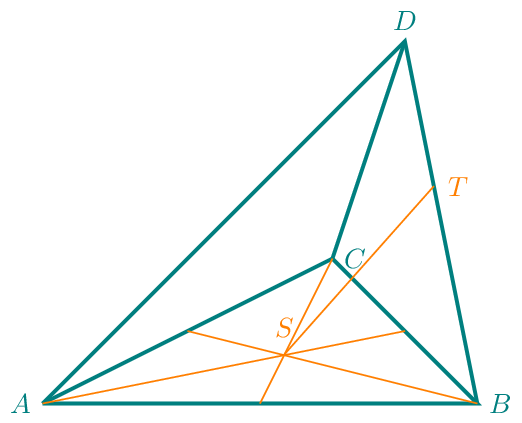
Stellen Sie den Vektor \(\overrightarrow{ST}\) als Linearkombination der Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) dar.

Aufgabe 7

Durch die Punkte \(A\), \(B\), \(C\), \(D\), \(E\) und \(F\) wird ein Pyramidenstumpf mit den Dreiecken \(ABC\) und \(DEF\) als Grund- und Deckfläche festgelegt. Grund- und Deckfläche sind zueinander parallel. Außerdem gilt: \(\frac{\left|\overline{DE}\right|}{\left|\overline{AB}\right|}=\frac{\left|\overline{EF}\right|}{\left|\overline{BC}\right|}=\frac{\left|\overline{DF}\right|}{\left|\overline{AC}\right|}=\frac{3}{5}\). Der Punkt \(M\) ist Mittelpunkt der Strecke \(\overline{BC}\) und der Punkt \(S\) ist Schwerpunkt des Dreiecks \(DEF\). Weiter gilt: \(\overrightarrow{AB}=\vec{a}\), \(\overrightarrow{AC}=\vec{b}\) und \(\overrightarrow{AD}=\vec{c}\).

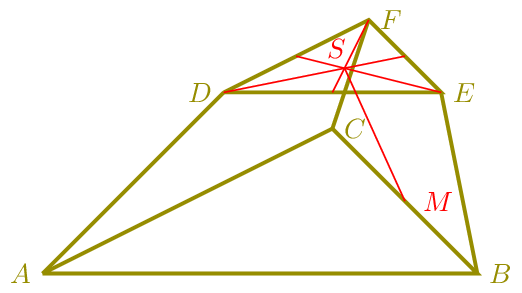
Stellen Sie den Vektor \(\overrightarrow{MS}\) als Linearkombination der Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) dar.

Aufgabe 8

Durch die Punkte \(A\), \(B\), \(C\), \(D\), \(E\) und \(F\) wird ein Prisma mit den Dreiecken \(ABC\) und \(DEF\) als Grund- und Deckfläche festgelegt. Der Punkt \(S\) ist der Schwerpunkt der Deckfläche \(DEF\) und der Punkt \(T\) ist Mittelpunkt des Parallelogramms \(CBEF\). Weiter gilt: \(\overrightarrow{AB}=\vec{a}\), \(\overrightarrow{AC}=\vec{b}\) und \(\overrightarrow{AD}=\vec{c}\).

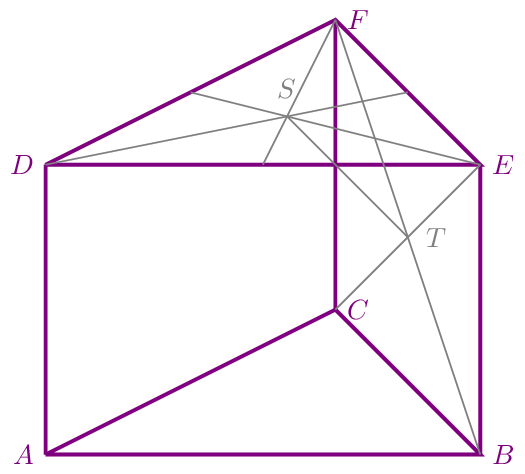
Stellen Sie den Vektor \(\overrightarrow{ST}\) als Linearkombination der Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) dar.