Integralrechnung¶
Die Integralrechnung behandelt nicht das Verhalten von Funktionen wie die Differenzialrechnung, sondern sie beschäftigt sich mit der Lösung einer speziellen Aufgabe, die man als Flächenproblem bezeichnet. Es handelt sich dabei um die Definition und die Berechnung der Maßzahl des Flächeninhalts eines beliebigen ebenen Flächenstücks. Auf den ersten Blick scheinen deshalb die beiden Hauptteile der Analysis, Differential- und Integralrechnung, grundverschieden zu sein, doch wird sich bald zeigen, dass ein überraschend enger Zusammenhang zwischen ihnen besteht.
Das unbestimmte Integral
Eine reelle Funktion \(F\) heißt Stammfunktion einer reellen Funktion \(f\) in einem Intervall \(I\subseteq D_{f}\) und \(I\subseteq D_{F^{\prime }}\), wenn gilt:
\(\frac{d}{dx}F(x)=F^{\prime }(x)=f(x)\) für alle \(x\in I\).
Stammfunktionen haben folgende Eigenschaften:
- Ist \(F_{1}\) eine Stammfunktion der Funktion \(f\) und \(C\in \mathbb{R}\) eine beliebige Konstante, so ist auch die Funktion \(F_{2}:x\mapsto F_{1}(x)+C\) mit \(D_{F_{2}}=D_{F_{1}}\) eine Stammfunktion der Funktion \(f\).
- Sind \(F_{1}\) und \(F_{2}\) zwei unterschiedliche Stammfunktionen einer Funktion \(f\) im gleichen Intervall \(I\), so unterscheiden sich \(F_{1}\) und \(F_{2}\) nur durch eine additive Konstante \(C\in \mathbb{R}\) und es gilt: \(F_{1}(x)=F_{2}(x)+C\) für alle \(x\in I\).
Aus den beiden Eigenschaften folgt, dass eine Funktion \(f\), die eine Stammfunktion \(F\) besitzt, nicht nur eine, sondern unendlich viele Stammfunktionen besitzt. Die Menge aller Stammfunktionen einer Funktion \(f\) in einem Intervall \(I\) wird mit \(\int f(x)dx\) bezeichnet und es gilt:
Der Term \(\int f(x)dx\) heißt dabei unbestimmtes Integral von \(f\). Ist die Funktion \(F_{1}\) irgend eine Stammfunktion der Funktion \(f\) in einem Intervall \(I\), so gilt:
Die Integration wird bei ganzrationalen Funktionen mit Hilfe folgender Integrationsregeln durchgeführt:
- Faktorregel: \(\int c\cdot f(x)dx=c\cdot\int f(x)dx\)
- Summenregel: \(\int(f(x)\pm g(x))dx=\int f(x)dx\pm\int g(x)dx\)
- Potenzregel: \(\int x^{n}dx=\frac{1}{n+1}x^{n+1}\) mit \(n\in\mathbb{R}\setminus\{-1\}\)
Das bestimmte Integral
Sei \(F\) eine beliebige Stammfunktion der Funktion \(f\). Dann gilt:
\(\int\limits_{a}^{b}f(x)dx\in \mathbb{R}\), ist also eine reelle Zahl und heißt bestimmtes Integral der Funktion \(f\) mit der Obergrenze \(b\) und der Untergrenze \(a\).
Eigenschaften des bestimmten Integrals:
- \(\int\limits_{a}^{b}f(x)dx=-\int\limits_{b}^{a}f(x)dx\)
- \(\int\limits_{a}^{b}f(x)dx=\int\limits_{a}^{c}f(x)dx+\int\limits_{c}^{b}f(x)dx\) mit \(a<c<b\)
- \(\int\limits_{a}^{b}kf(x)dx=k\int\limits_{a}^{b}f(x)dx\) mit \(k\in \mathbb{R}\)
- \(\int\limits_{a}^{b}\left( f(x)\pm g(x)\right)dx=\int\limits_{a}^{b}f(x)dx\pm \int\limits_{a}^{b}g(x)dx\)
Das bestimmte Integral hat folgende geometrische Bedeutung:
Sind \(f\) und \(g\) zwei stetige Funktionen in einem Intervall \(\left[a;b\right]\) mit \(a<b\) und gilt \(f(x)\geq g(x)\) für alle \(x\in\left[a;b\right]\), so ist \(\int\limits_{a}^{b}(f(x)-g(x))dx\geq0\).
Außerdem ist in diesem Fall \(\int\limits_{a}^{b}(f(x)-g(x))dx\) ist die Maßzahl des Flächeninhalts der Fläche, die von \(G_{f}\), \(G_{g}\) und den vertikalen Geraden mit den Gleichungen \(x=a\) und \(x=b\) eingeschlossen ist.
Gilt hingegen \(f(x)\leq g(x)\) für alle \(x\in\left[a;b\right]\), so ist \(\int\limits_{a}^{b}(f(x)-g(x))dx\leq0\). In diesem Fall wird die Maßzahl des Flächeninhalts der Fläche, die von \(G_{f}\), \(G_{g}\) und den vertikalen Geraden mit den Gleichungen \(x=a\) und \(x=b\) eingeschlossen ist, mit \(-\int\limits_{a}^{b}(f(x)-g(x))dx\) berechnet.
Im Allgemeinen ist der Wert des bestimmten Integrals \(\int\limits_{a}^{b}(f(x)-g(x))dx\) eine Flächenbilanz zwischen den Flächen, bei denen \(G_{f}\) oberhalb \(G_{g}\) (positiver Wert) und den Flächen, bei denen \(G_{f}\) unterhalb \(G_{g}\) (negativer Wert) verläuft. Setzt man \(g(x)=0\), so werden mit \(\int\limits_{a}^{b}f(x)dx\) Flächenbilanzen für Flächen betrachtet, die \(G_{f}\) mit der \(x\)-Achse bestimmt.
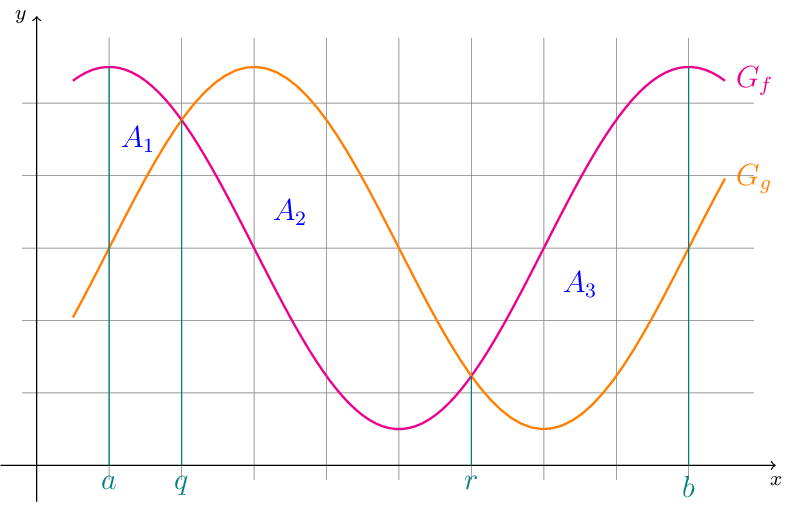
Die Maßzahl des Flächeninhalts der Flächen, die von \(G_{f}\), \(G_{g}\) und den vertikalen Geraden mit den Gleichungen \(x=a\) und \(x=b\) eingeschlossen ist berechnet sich hier mit: