Definitionslücken und Asymptoten

• Aufgaben

Eine Funktion \(f\) der Form

\[f:x\mapsto\dfrac{a_{m}x^{m}+\ldots+a_{2}x^{2}+a_{1}x+a_{0}}{b_{n}x^{n}+\ldots+b_{2}x^{2}+b_{1}x+b_{0}}\]

heißt gebrochen-rationale Funktion, falls der Nenner des Funktionsterms \(f(x)\) die Variable \(x\) enthält. Der Zähler der Funktion \(f\) ist der Term \(Z(x)=a_{m}x^{m}+\ldots+a_{2}x^{2}+a_{1}x+a_{0}\), ein Polynom mit Grad \(m\) und der Nenner der Funktion \(f\) ist der Term \(N(x)=b_{n}x^{n}+\ldots+b_{2}x^{2}+b_{1}x+b_{0}\), ein Polynom mit Grad \(n\).

Der maximale Definitionsbereich \(D_{f}\) der Funktion \(f\) ist eine Teilmenge von \(\mathbb{R}\), also \(D_{f}\subseteq\mathbb{R}\). Falls nichts weiter gesagt, ist mit \(D_{f}\) der in \(\mathbb{R}\) größtmögliche Definitionsbereich gemeint.

Standardbeispiel 1

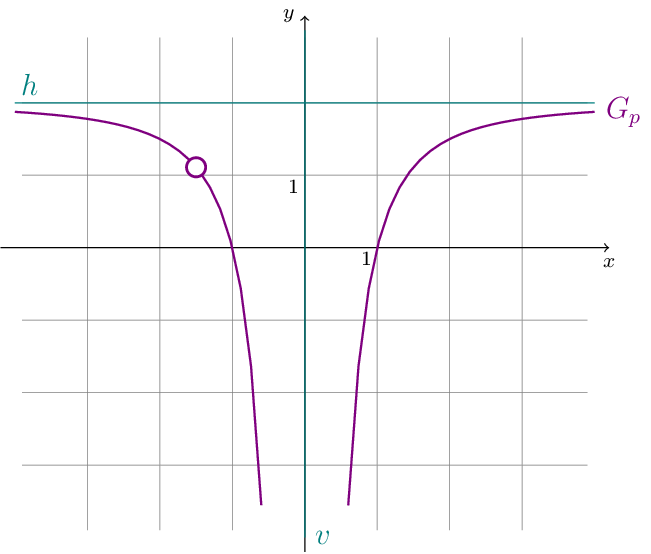
Gegeben ist die Funktion \(h:x\mapsto\dfrac{7x-7}{5x^{2}-10x-15}\).

Für den Zähler gilt: \(Z(x)=7x-7\), also ist der Zählergrad \(1\). Für den Nenner gilt: \(N(x)=5x^{2}-10x-15\), also ist der Nennergrad gleich \(2\).

Da der Nennergrad größer als der Zählergrad ist, handelt es bei \(h\) um eine echt gebrochen-rationale Funktion.

Mit der Lösungsformel lösen wir die Gleichung \(N(x)=0\) und erhalten \(x_{1}=-1\) und \(x_{2}=3\). Das bedeutet, dass der Nenner an diesen Stellen Null ist, also ist \(h\) an diesen Stellen nicht definiert. Somit können wir den Definitionsbereich \(D_{h}\) von \(h\) angeben, nämlich \(D_{h}=\mathbb{R}\setminus\{-1;3\}\) und \(-1\) und \(3\) sind die Definitionslücken von \(h\).

Allgemein gilt:

Die größtmögliche Definitionsmenge \(D_{f}\) einer gebrochen-rationalen Funktion \(f\) ist die Zahlenmenge:

\(D_{f}=\mathbb{R}\setminus\{x|N(x)=0\}\).

Setzen wir nun den Zähler von \(h\) gleich Null, also \(Z(x)=0\) und lösen die Gleichung, so erhalten wir: \(7x-7=0\), oder \(x=1\). Wir stellen fest: \(1\in D_{h}\) und \(h(1)=0\), also ist \(x=1\) die Nullstelle von \(h\).

Allgemein gilt:

Für eine Nullstelle \(x_{0}\) einer gebrochen-rationalen Funktion \(f\) gilt:

\(Z(x_{0})=0\) und \(x_{\text{0}}\in D_{f}\).

---

Mit Hilfe der Grenzwertberechnung untersuchen wir das Verhalten von \(h(x)\) im Unendlichen und bei Annäherung von \(x\) an die Definitionslücken.

\(\underset{x\rightarrow\infty}{\lim}h(x)=\underset{x\rightarrow\infty}{\lim}\dfrac{7x-7}{5x^{2}-10x-15}=\underset{x\rightarrow\infty}{\lim}\dfrac{7x}{5x^{2}}=\underset{x\rightarrow\infty}{\lim}\dfrac{7}{5x}=0\)

\(\underset{x\rightarrow-\infty}{\lim}h(x)=\underset{x\rightarrow-\infty}{\lim}\dfrac{7x-7}{5x^{2}-10x-15}=\underset{x\rightarrow-\infty}{\lim}\dfrac{7x}{5x^{2}}=\underset{x\rightarrow-\infty}{\lim}\dfrac{7}{5x}=0\)

Bemerkung

Bei der Grenzwertberechnung \(\underset{x\rightarrow\pm\infty}{\lim}f(x)\) werden im Zähler und Nenner immer nur die dominanten Summanden verwendet. Alle anderen Summanden haben keinen Einfluss auf diesen Grenzwert.

Für den Graphen \(G_{h}\) der Funktion \(h\) bedeutet die obige Grenzwertberechnung, dass im Unendlichen die \(y\)-Koordinaten der Punkte von \(G_{h}\) sich dem Wert Null annähern, also nähert sich im Unendlichen \(G_{h}\) der \(x\)-Achse an. Man sagt dazu, dass die \(x\)-Achse eine waagerechte Asymptote von \(G_{h}\) ist.

Allgemein gilt:

Nähern sich im Unendlichen die Funktionswerte einer gebrochen-rationalen Funktion \(f\) einem bestimmten Wert \(a\) an, so ist die waagerechte Gerade mit der Gleichung \(y=a\) eine waagerechte Asymptote des Graphen \(G_{f}\) der Funktion \(f\).

---

Bei der Untersuchung des Verhaltens von \(h(x)\) bei Annäherung von \(x\) an die Definitionslücken wird die links- und die rechtsseitig Annäherung an die Definitionslücke betrachtet.

Rechtsseitige Annäherung an \(3\):

\[\underset{x\rightarrow3^{+}}{\lim}\dfrac{\overset{\rightarrow14}{\overbrace{7x-7}}}{\underset{\rightarrow0^{+}}{\underbrace{5x^{2}-10x-15}}}=+\infty\]

Linksseitige Annäherung an \(3\):

\[\underset{x\rightarrow3^{-}}{\lim}\dfrac{\overset{\rightarrow14}{\overbrace{7x-7}}}{\underset{\rightarrow0^{-}}{\underbrace{5x^{2}-10x-15}}}=-\infty\]

Rechtsseitige Annäherung an \(-1\):

\[\underset{x\rightarrow-1^{+}}{\lim}\dfrac{\overset{\rightarrow-14}{\overbrace{7x-7}}}{\underset{\rightarrow0^{+}}{\underbrace{5x^{2}-10x-15}}}=+\infty\]

Linksseitige Annäherung an \(-1\):

\[\underset{x\rightarrow-1^{-}}{\lim}\dfrac{\overset{\rightarrow-14}{\overbrace{7x-7}}}{\underset{\rightarrow0^{-}}{\underbrace{5x^{2}-10x-15}}}=-\infty\]

Bemerkung

Bei der Grenzwertberechnung \(\underset{x\rightarrow\pm p}{\lim}f(x)\) werden in den Zähler und in den Nenner von \(f(x)\) Werte eingesetzt, die nahe an \(p\) liegen.

Bei links- und rechtsseitiger Annäherung an \(-1\) nehmen die Funktionswerte von \(h\) die Werte \(-\infty\) oder \(+\infty\) an. Außerdem ändert sich das Vorzeichen von \(h(x)\) an der Stelle \(-1\). Man sagt dazu, dass die Stelle \(x=-1\) eine Polstelle mit Vorzeichenwechsel ist. Für den Graphen \(G_{h}\) bedeutet dies, dass er sich in einer sehr nahen Umgebung um \(-1\) der senkrechten Geraden \(G_{v_{1}}\) mit der Gleichung \(v_{1}:x=3\) annähert. Diese Gerade ist somit eine senkrechte Asymptote von \(G_{h}\). Genauso ist \(x=3\) eine Polstelle mit Vorzeichenwechsel und die Gerade \(G_{v_{2}}\) mit der Gleichung \(v_{2}:x=3\) ist eine senkrechte Asymptote von \(G_{h}\).

Allgemein gilt:

Ist die Stelle \(x=p\) eine Polstelle der Funktion \(f\), so hat \(G_{f}\) die senkrechte Asymptote mit der Gleichung \(v: x=p\). Es gibt Polstellen mit und ohne Vorzeichenwechsel.

Der Graph \(G_{h}\) hat eine waggerechte Asymptote und zwei senkrechte Asymptoten.

Standardbeispiel 2

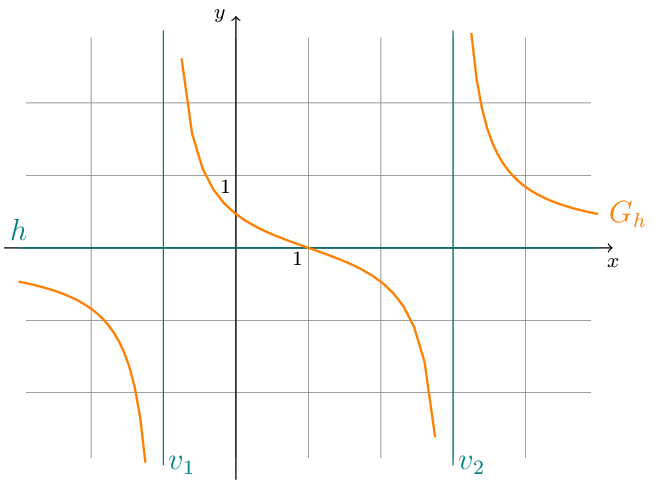
Gegeben ist die Funktion \(k:x\mapsto\dfrac{2x^{3}-11x^{2}+20x+33}{3x^{2}-12x+12}\).

Bei der Funktion \(k\) ist der Zählergrad \(3\) und der Nennergrad \(2\). Somit handelt es sich bei der Funktion \(k\) um eine unecht gebrochen-rationale Funktion.

Allgemein gilt:

Ist bei einer gebrochen-rationalen Funktion \(f\) der Zählergrad größer oder gleich dem Nennergrad, so liegt eine unecht gebrochen-rationale Funktion vor.

Wir setzten \(N(x)=3x^{2}-12x+12\) und lösen die Gleichung \(N(x)=0\). Man erhält die doppelte Lösung \(x_{1,2}=2\). Der Definitionsbereich ist somit \(D_{k}=\mathbb{R}\setminus\{2\}\).

Der Zähler von \(k(x)\) ist der Term \(Z(x)=2x^{3}-11x^{2}+20x+33\). Die Lösungen der Gleichung \(Z(x)=0\) erhalten wir mit Hilfe der Polynomdivision ohne Rest.

Mit dem Taschenrechner berechnen wir \(Z(-1)=0\) und die Polynomdivision ohne Rest ergibt:

\[(2x^{3}-11x^{2}+20x+33):(x+1)=2x^{2}-13x+33\text{.}\]

Wir stellen fest, dass \(Z(x)\) nicht weiter in Linearfaktoren zerlegt werden kann, da die Diskriminante des quadratischen Terms negativ ist. Somit ist \(x_{1}=-1\) die einzige Nullstelle von \(k\). Der Funktionsterm \(k(x)\) kann nun in Linearfaktoren zerlegt angegeben werden. Er hat die Form:

\[k(x)=\dfrac{(x+1)(2x^{2}-13x+33)}{3(x-2)^{2}}\text{.}\]

Wie schon oben erwähnt, ist die Funktion \(k\) eine unecht gebrochen-rationale Funktion. Der Term \(k(x)\) kann somit mit Hilfe der Polynomdivision mit Rest umgeformt werden. Die Polynomdivision mit Rest liefert:

\((2x^{3}-11x^{2}+20x+33):(3x^{2}-12x+12)=\frac{2}{3}x-1+\dfrac{15}{(x-2)^{2}}\).

Es gilt also: \(k(x)=\frac{2}{3}x-1+\dfrac{15}{(x-2)^{2}}\). Wir sehen, dass \(k(x)\) den ganzrationalen Anteil \(\frac{2}{3}x-1\) und den echt gebrochen-rationalen Anteil \(\dfrac{15}{(x-2)^{2}}\) hat.

Für den echt gebrochen-rationalen Anteil berechnen wir:

\[\underset{x\rightarrow\pm\infty}{\lim}\dfrac{15}{(x-2)^{2}}=\underset{x\rightarrow\pm\infty}{\lim}\dfrac{15}{x^{2}}=0\]

Das bedeutet, dass im Unendlichen der echt gebrochen-rationale Anteil fast keinen Einfluss auf die \(y\)-Koordinaten der Punkte von \(G_{k}\) hat. \(G_{k}\) verläuft im Unendlichen sehr nahe an der Geraden \(G_{s}\) mit der Gleichung \(s:y=\frac{2}{3}x-1\). Diese Gerade ist somit eine schräge Asymptote von \(G_{k}\).

Allgemein gilt:

Ist bei einer gebrochen-rationalen Funktion \(f\) der Zählergrad um \(1\) größer als der Nennergrad, so besitzt der Graph \(G_{f}\) dieser Funktion \(f\) eine schräge Asymptote. Die Gleichung der schrägen Asymptote ermittelt man mit Hilfe der Polynomdivision mit Rest.

Neben der schrägen Asymptote könnte \(G_{k}\) auch eine senkrechte Asymptote besitzen. Dazu untersuchen wir das Verhalten von \(k(x)\) bei Annäherung von \(x\) an die Definitionslücke \(x=2\):

\[ \begin{align}\begin{aligned}\underset{x\rightarrow2^{+}}{\lim}\dfrac{\overset{\rightarrow44}{\overbrace{2x^{3}-11x^{2}+20x+33}}}{\underset{\rightarrow0^{+}}{\underbrace{3x^{2}-12x+12}}}=+\infty\text{,}\\\underset{x\rightarrow2^{-}}{\lim}\dfrac{\overset{\rightarrow44}{\overbrace{2x^{3}-11x^{2}+20x+33}}}{\underset{\rightarrow0^{+}}{\underbrace{3x^{2}-12x+12}}}=+\infty\text{.}\end{aligned}\end{align} \]

Die Stelle \(x=2\) ist somit eine Polstelle ohne Vorzeichenwechsel und \(G_{k}\) hat die senkrechte Asymptote mit der Gleichung \(v:x=2\).

Standardbeispiel 3

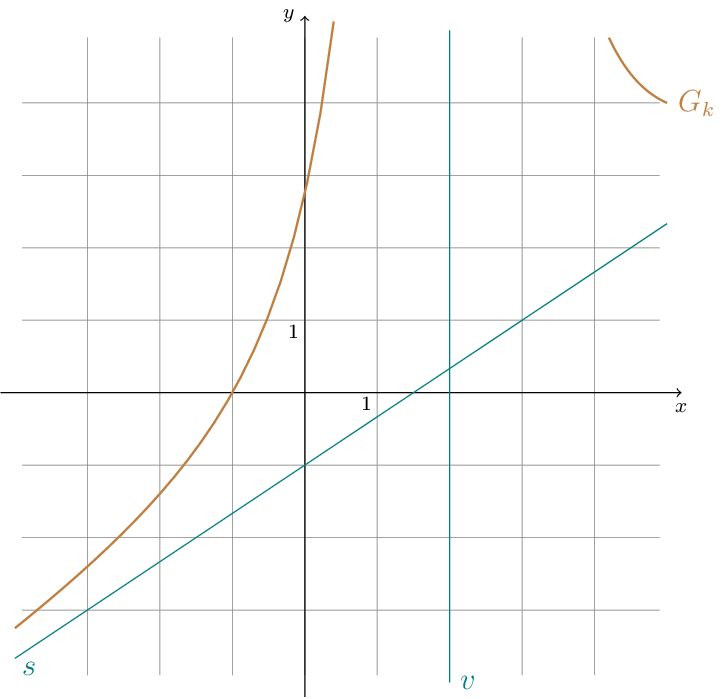
Gegeben ist die Funktion \(p:x\mapsto\dfrac{4x^{3}+6x^{2}-4x-6}{2x^{3}+3x^{2}}\).

Bei der Funktion \(p\) ist der Zählergrad \(3\) und der Nennergrad \(3\). Somit handelt es sich bei der Funktion \(p\) um eine unecht gebrochen-rationale Funktion.

Wir setzen \(N(x)=2x^{3}+3x^{2}\) und lösen die Gleichung \(N(x)=0\). Damit bestimmen wir den Definitionsbereich \(D_{p}\).

\(N(x)=0\) ; \(2x^{3}+3x^{2}=0\),

\(x^{2}(2x+3)=0\) ; \(x_{1,2}=0\) und \(x_{3}=-\frac{3}{2}\).

Definitionsbereich: \(D_{p}=\mathbb{R}\setminus\{-\frac{3}{2};0\}\)

Als nächstes setzten wir \(Z(x)=4x^{3}+6x^{2}-4x-6\) und lösen die Gleichung \(Z(x)=0\), um die Nullstellen von \(p\) zu erhalten.

\(Z(x)=0\) ; \(4x^{3}+6x^{2}-4x-6=0\) ; TR: \(x_{0}=1\)

Polynomdivision ohne Rest ergibt:

\((4x^{3}+6x^{2}-4x-6):(x-1)=4x^{2}+10x+6\)

\(4x^{2}+10x+6=0\)

\(x_{2,3}=\frac{-10\pm2}{8}\) ; \(x_{2}=-1\), \(x_{3}=-\frac{3}{2}\notin D_{p}\)

\(x_3=-\frac{3}{2}\) ist keine Nullstelle von \(p\).

Die Nullstellen von \(p\) sind \(x_{1}=1\) und \(x_{2}=-1\).

Die Linearfaktorenzerlegung von \(p(x)\) zeigt, dass im Zähler und Nenner gleiche Linearfaktoren erscheinen. Es kann also gekürzt werden.

\[p(x)=\dfrac{4(x-1)(x+1)(x+\frac{3}{2})}{2x^{2}(x+\frac{3}{2})}=\dfrac{2(x-1)(x+1)}{x^{2}}\]

Der Linearfaktor \(x+\frac{3}{2}\) verschwindet nach dem Kürzen aus dem Nenner. Trotzdem bleibt der Definitionsbereich \(D_{p}\) unverändert und \(x=-\frac{3}{2}\) ist weiterhin eine Definitionslücke. In diesem Fall ist es eine stetig behebbare Definitionslücke. Alle weiteren Berechnungen werden mit dem gekürzten Funktionsterm \(p(x)=\dfrac{2(x-1)(x+1)}{x^{2}}\) durchgeführt und der unveränderte Definitionsbereich \(D_{p}=\mathbb{R}\setminus\{-\frac{3}{2};0\}\) beachtet.

Allgemein gilt:

Erscheinen bei einer gebrochen-rationalen Funktion \(f\) im Zähler und im Nenner gleiche Faktoren, so darf gekürzt werden. Verschwindet dabei ein Linearfaktor aus dem Nenner, so hat die Funktion an der entsprechenden Stelle eine stetig behebbare Definitionslücke.

Das Verhalten von \(p(x)\) bei Annäherung von \(x\) an die Definitionslücken zeigt bei der Funktion \(p\) unterschiedliches Verhalten.

\[\underset{x\rightarrow0^{+}}{\lim}\dfrac{\overset{\rightarrow-2}{\overbrace{2(x-1)(x+1)}}}{\underset{\rightarrow0^{+}}{\underbrace{x^{2}}}}=-\infty\text{ ; }\underset{x\rightarrow0^{-}}{\lim}\dfrac{\overset{\rightarrow-2}{\overbrace{2(x-1)(x+1)}}}{\underset{\rightarrow0^{+}}{\underbrace{x^{2}}}}=-\infty\]

Die Stelle \(x=0\) ist eine Polstelle ohne Vorzeichenwechsel.

\[\underset{x\rightarrow-\frac{3}{2}^{+}}{\lim}\dfrac{\overset{\rightarrow\frac{5}{2}}{\overbrace{2(x-1)(x+1)}}}{\underset{\rightarrow\frac{9}{4}}{\underbrace{x^{2}}}}=\frac{10}{9}\text{ ; }\underset{x\rightarrow-\frac{3}{2}^{-}}{\lim}\dfrac{\overset{\rightarrow\frac{5}{2}}{\overbrace{2(x-1)(x+1)}}}{\underset{\rightarrow\frac{9}{4}}{\underbrace{x^{2}}}}=\frac{10}{9}\]

Wir erkennen, dass das Ergebnis bei diesem Grenzwert eine feste Zahl und nicht \(-\infty\) oder \(+\infty\) ist. Das ist ein Nachweis dafür, dass die Stelle \(x=-\frac{3}{2}\) eine stetig behebbare Definitionslücke ist.

Da die Funktion \(p\) eine unecht gerochen-rationale Funktion ist, lässt sich der Funktionsterm \(p(x)\) mit Hilfe der Polynomdivision mit Rest umformen.

Wir erhalten: \((2x^{2}-2):x^{2}=2-\dfrac{2}{x^{2}}\).

Es gilt also \(p(x)=2-\dfrac{2}{x^{2}}\).

Der echt gerochen-rationale Anteil ist \(\dfrac{2}{x^{2}}\) und

\[\underset{x\rightarrow-\infty}{\lim}\dfrac{2}{x^{2}}=\underset{x\rightarrow+\infty}{\lim}\dfrac{2}{x^{2}}=0\text{.}\]

Damit nähern sich die Funktionswerte \(p(x)\) im Unendlichen der Zahl \(2\) an und die Gerade \(G_{h}\) mit der Gleichung \(h:y=2\) ist eine waagerechte Asymptote von \(G_{p}\).