Aufgaben¶
Aufgabe 1¶
Untersuchen Sie das Verhalten folgender Funktionen an den Rändern des Definitionsintervalls. Geben Sie an, ob ein Randextremum existiert und ermitteln Sie, ob am Rand ein Hoch- oder Tiefpunkt vorliegt.
\(f(x)=\frac{3}{5}x+7\) ; \(D_{f}=\mathbb{R}\)
\(g(x)=-\frac{1}{3}x^{2}+\frac{4}{5}x-\frac{12}{5}\) ; \(D_{g}=\left]-4;\frac{7}{4}\right[\)
\(h(x)=\frac{3}{5}x^{3}-4x^{2}+\frac{8}{7}x-3\) ; \(D_{h}=\mathbb{R}\)
\(i(x)=-\frac{1}{16}x^{4}+\frac{5}{6}x^{3}-2x^{2}-\frac{5}{11}x+2\) ; \(D_{i}=\left[-\frac{3}{2};\frac{4}{3}\right[\)
\(j(x)=-\frac{7}{4}x+\frac{2}{3}\) ; \(D_{j}=\left]-\infty;3\right]\)
\(k(x)=3x^{3}-\frac{1}{5}x+\frac{20}{13}\) ; \(D_{k}=\left]4;\infty\right[\)
\(l(x)=-\frac{2}{5}(x+1)(x-4)(3x^{2}+5)\) ; \(D_{l}=\left]-\infty;8\right]\)
\(m(x)=\frac{3}{4}(x+2)(2x^{2}+7)\) ; \(D_{m}=\left[-3;\infty\right[\)
\(n(x)=\frac{3}{5}(x+2)(x-4)\) ; \(D_{n}=\left[-4;1\right[\cup\left]1;\infty\right[\)
Aufgabe 2¶
Gegeben ist die Funktion \(f(x)=\frac{1}{12}x^{4}-\frac{1}{2}x^{3}+\frac{4}{9}x^{2}+\frac{110}{81}x-\frac{100}{81}\) mit \(x\in\mathbb{R}\). \(G_{f}\) berührt die \(x\)-Achse an der Stelle \(x_{0}=\frac{10}{3}\).
Berechnen Sie die drei Nullstellen von \(f\).
Untersuchen Sie das Monotonieverhalten von \(G_{f}\).
Bestimmen Sie Art und Koordinaten der Extrempunkte von \(G_{f}\).
Untersuchen Sie das Krümmungsverhalten von \(G_{f}\).
Berechnen Sie die Koordinaten der Wendepunkte von \(G_{f}\).
Skizzieren Sie mit Hilfe der gewonnenen Erkenntnisse einen möglichen Verlauf von \(G_{f}\).
\(G_{f}\) und die \(x\)-Achse schließen zwei endliche Flächen ein. Berechnen Sie die Flächenzahl dieser Flächen gerundet auf zwei Stellen nach dem Komma.
Aufgabe 3¶
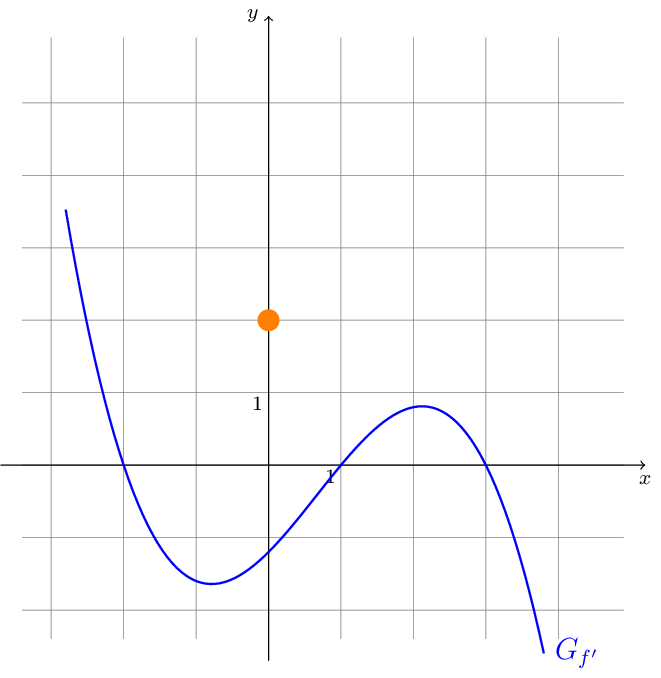
Gegeben ist \(G_{f^{\prime}}\) und ein Punkt von \(G_{f}\).
Skizzieren Sie \(G_{f}\) und \(G_{f^{\prime\prime}}\).
Aufgabe 4¶
Gegeben ist die Funktion \(f(x)=x^{4}-4x^{3}+4x^{2}\) mit \(x\in\mathbb{R}\).
Berechnen Sie die Nullstellen von \(f\).
Ermitteln Sie Art, Koordinaten der Extrempunkte und die Wendepunkte von \(G_{f}\).
Skizzieren Sie \(G_{f}\) für \(-0.5\leq x\leq2.5\).
Gegeben ist die Funktion mit dem Term \(p(x)=\frac{4}{9}x^{2}\) mit \(x\in\mathbb{R}\). Der Graph von \(p\) ist die Parabel \(G_{p}\). \(G_{p}\), die \(x\)-Achse und der Teil von \(G_{f}\), der rechts vom Punkt \(N(2;0)\) liegt, schließen eine endliche Fläche ein.
Markieren Sie diese Fläche mit einer Kontur und berechnen Sie die Flächenzahl dieser Fläche gerundet auf zwei Stellen nach dem Komma.
Aufgabe 5¶
Aufstellen von Funktionstermen aus gegebenen Eigenschaften
Der Graph von \(f(x)=ax^{3}+bx^{2}+c\) soll im Wendepunkt \(W(-1;1)\) die Steigung \(-3\) haben. Bestimmen Sie \(f(x)\).
Gesucht ist eine ganzrationale Funktion von möglichst kleinem Grad, deren Graph symmetrisch zum Ursprung ist und den Extrempunkt \(E( 3;-18)\) hat.
Der Graph einer ganzrationalen Funktion dritten Grades verläuft durch den Punkt \(P(1;-4)\), hat an der Stelle \(x=4\) eine horizontale Tangente und den Wendepunkt \(W(3;-6)\). Bestimmen Sie den Funktionsterm.
Gesucht ist die Gleichung einer ganzrationalen Funktion vierten Grades mit der Wendetangentengleichung \(t:y=-16x+27\) in der Wendestelle \(x=1\) und der doppelten Nullstelle \(x=2\).
Wie lautet die Gleichung einer ganzrationalen Funktion dritten Grades deren Graph den Wendepunkt \(W(-2;9)\) und den Tiefpunkt \(T(-4;-7)\) hat?
Die Wendetangente des Graphen einer ganzrationalen Funktion dritten Grades schneidet die \(y\)-Achse bei \(y=-3\). Der Graph hat den Wendepunkt \(W(2;1)\) und die Nullstelle \(x=1\).
Aufgabe 6¶
Lösen Sie folgende Anwendungsaufgaben.
Eine zylinderförmige Trommel besitzt die Gesamtoberfläche \(7536\,\mathrm{cm^{2}}\). Der Klang der Trommel hängt auch von der Oberfläche und dem Volumen ab. Die Boden- und Deckfläche der Trommel sind mit Fell bespannt. Durch die erhältlichen Fellgrößen ergibt sich, dass ein Radius \(r\) von \(12\,\mathrm{cm}\) bis \(30\,\mathrm{cm}\) möglich ist. Führen Sie die folgenden Rechnungen ohne Einheiten durch. Stellen Sie eine Gleichung für das Volumen \(V(r)\) der Trommel in Abhängigkeit von \(r\) auf. Berechnen Sie \(r\) so, dass das Volumen \(V\) der Trommel den größten Wert (und damit die Trommel den tiefsten Ton) annimmt.
Die Gebührenordnung des Paketdienstes Paket Ahoi enthält folgende Klausel: Bei Päckchen in Zylinderform darf die Summe aus der Höhe \(h\) des Zylinders und dem Durchmesser \(d\) des Grundkreises \(100\,\mathrm{cm}\) nicht überschreiten. Auf Einheiten wird im Folgenden verzichtet. Berechnen Sie das Volumen \(V(d)\) eines solchen Päckchens, wenn die in der Gebührenordnung erwähnte Summe genau \(100\,\mathrm{cm}\) beträgt. Bestimmen Sie auch eine geeignete Definitionsmenge. Bestimmen Sie nun die Maße desjenigen zylinderförmigen Päckchens, das dabei maximales Volumen aufweist.
Aus einem Stück Draht der Länge \(72\,\mathrm{cm}\) sollen die Kanten eines Quaders geformt werden, dessen Grundfläche ein Rechteck mit den Seitenlängen \(a\) bzw. \(2a\) ist. Berechnen Sie zunächst das Volumen \(V(a)\) des Quaders in Abhängigkeit von der Länge \(a\). Bestimmen Sie auch eine sinnvolle Definitionsmenge. Bestimmen Sie nun denjenigen Wert von \(a\), für den das Volumen \(V\) des Quaders sein absolutes Maximum annimmt. Berechnen Sie auch das maximale Volumen.
Ein Doppelrundbogenfenster wird von drei Seiten eines Rechtecks sowie von zwei Halbkreisen (jeweils Radius \(r\)) begrenzt. Der Umfang des Fensters beträgt \(10\,\mathrm{m}\). Auf Einheiten wird in der Rechnung verzichtet. Stellen Sie den Flächeninhalt \(A(r)\) des Fensters in Abhängigkeit vom Radius \(r\) der Halbkreise dar und bestimmen Sie eine sinnvolle Definitionsmenge. Berechnen Sie auf 2 Nachkommastellen genau denjenigen Wert von \(r\), für den der Flächeninhalt des Fensters seinen größten Wert annimmt. Wie viel Prozent des Inhalts nimmt in diesem Fall der rechteckige Teil des Fensters ein?
In einen dreieckigen Dachgiebel soll symmetrisch zur Mittelachse (\(y\)-Achse) ein rechteckiges Fenster eingebaut werden. Das Fenster soll auf einem Sims der Höhe \(1\,\mathrm{m}\) aufsitzen. Die oberen Ecken des Fensters liegen auf den Kanten des Giebels. Der Giebel ist \(6\,\mathrm{m}\) hoch und \(16\,\mathrm{m}\) breit. Die Länge des Fensters beträgt \(2a\). Stellen Sie den Flächeninhalt \(A(a)\) des Fensters in Abhängigkeit von \(a\) dar und bestimmen Sie eine sinnvolle Definitionsmenge. Bestimmen Sie nun \(a\) so, dass der Flächeninhalt des Fensters den größten Wert annimmt. Ermitteln Sie auch Breite und Höhe dieses Fensters.
Gegenüber einem Würfel der Kantenlänge \(x\) sind die Kanten der Bodenfläche eines Quaders um \(3\,\mathrm{cm}\) größer, seine Höhe um \(3\,\mathrm{cm}\) geringer. Bestimmen Sie das Volumen \(V(x)\) des Quaders in Abhängigkeit von \(x\) und bestimmen Sie eine sinnvolle Definitionsmenge. Berechnen Sie die Kantenlänge \(x\) des Würfels so, dass Quader und Würfel gleiches Volumen haben.
Um Obstkisten aus Pappe herzustellen, werden aus rechteckigen Kartonplatten an den 4 Ecken jeweils Quadrate abgeschnitten. Anschließend werden die Seitenteile so gefalzt, dass doppelwandige Seiten mit der Höhe \(x\) entstehen. Die Kartonplatten haben zu Beginn eine Länge von \(1.20\,\mathrm{m}\) und eine Breite von \(0.90\,\mathrm{m}\). Stellen Sie die Maßzahl des Volumens \(V(x)\) einer solchen Obstkiste in Abhängigkeit von der Höhe \(x\) dar. Bestimmen Sie zudem eine sinnvolle Definitionsmenge. Bestimmen Sie nun \(x\) so, dass das Volumen der Kiste den größtmöglichen Wert annimmt. Berechnen Sie auch das maximale Volumen \(V_{max}\).
Herr K. plant den Einbau eines Dachfensters. Dieses soll die Form eines Rechtecks mit darübergesetztem gleichschenklig-rechtwinkligem Dreieck haben. Der Umfang \(U\) des gesamten Fensters beträgt \(6\,\mathrm{m}\). Stellen Sie zunächst die Maßzahl \(G(x)\) der Gesamtfläche des Fensters in Abhängigkeit von der Rechtecksbreite \(x\) dar. Ermitteln Sie auch die Definitionsmenge der Funktion \(G\). Berechnen Sie dann denjenigen Wert von \(x\), für den die Flächenmaßzahl \(G(x)\) ihren absolut größten Wert annimmt. Runden Sie dabei auf zwei Nachkommastellen.
Aufgabe 7¶
Auf dem Außengelände des Kindergartens St. Josep soll eine neue Sandfläche gemäß folgender Skizze angelegt werden.
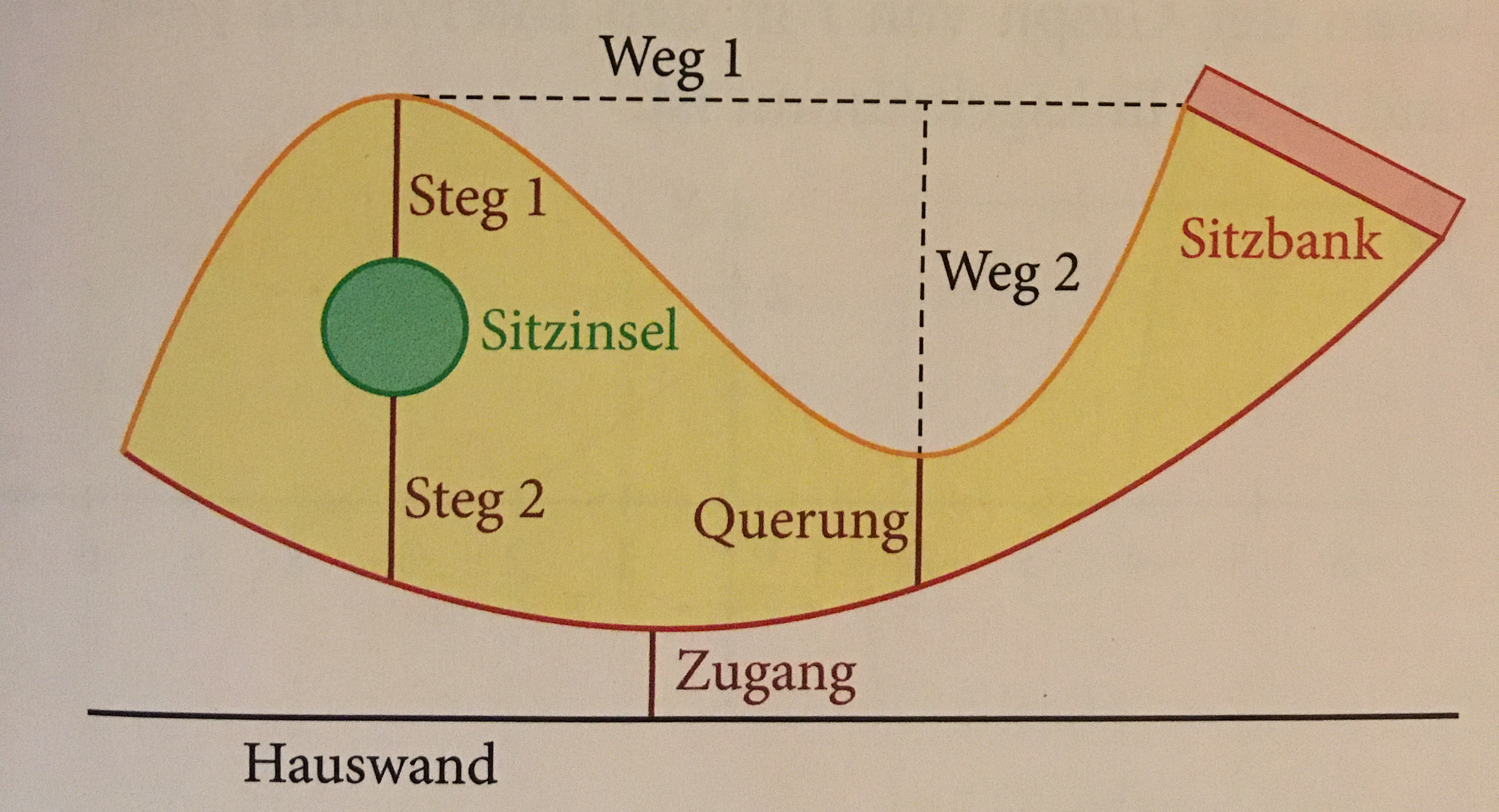
Sandfläche¶
Den beiden Begrenzungen liegen die folgenden Funktionen zugrunde:
\(g(x)=\frac{1}{48}x^{3}-\frac{1}{2}x^{2}+3x+4\) und
\(f(x)=\frac{1}{24}x^{2}-\frac{2}{3}x+4\) mit \(x\in\mathbb{R}\).
Die Sitzinsel ist ein Kreis mit einem Durchmessermaß von \(2\).
Das Längenmaß des Abstandes zwischen Kreismittelpunkt und Hauswand hat den Wert \(6\).
Die Sitzbank steht senkrecht auf die obere Kurve.
Berechnen Sie folgende Längenmaßzahlen: Zugang, Sitzbank, Querung, Stege und Wege.
Prüfen Sie, ob die Querung die kürzeste senkrechte Verbindung zwischen den beiden Kurven im dargestellten Bereich ist.
Der Sandplatz soll mit einer \(40\,\mathrm{cm}\) dicken Sandschicht aufgefüllt werden. Wie viel kostet der Sand, wenn mit einer Dichte des Sandes von \(1.40\,\mathrm{\frac{t}{m^{3}}}\) und mit einem Preis von \(25\) Euro pro Tonne gerechnet wird?
Aufgabe 8¶
Gegeben sind die Funktionen
\(h_{a}(x)=\frac{1}{4}ax^{3}-\frac{4}{3}x^{2}+\frac{3}{2}x-2a+\frac{7}{3}\) mit \(a,x\in\mathbb{R}\) und \(a\neq0\).
Zeigen Sie, dass \(x=2\) eine Nullstelle von \(h_{a}\) ist und berechnen Sie denjenigen Wert von \(a\), für den \(x=2\) eine doppelte Nullstelle von \(h_{a}\) ist.
Untersuchen Sie die Monotonie von \(h_{a}\) in Abhängigkeit von \(a\) für \(a>2\).
Untersuchen Sie das Verhalten von \(h_{a}(x)\) im Unendlichen \(a<0\).
Berechnen Sie den Wert von \(a\), so dass gilt: \(\int\limits_{2}^{6}h_{a}(x)dx=-\frac{208}{9}\).
Für \(a=\frac{1}{2}\) haben wir die Funktion \(h_{0.5}(x)\), die wir kurz mit \(h(x)\) bezeichnen. Es gilt \(h(x)=\frac{1}{8}x^{3}-\frac{4}{3}x^{2}+\frac{3}{2}x+\frac{4}{3}\) mit \(x\in\mathbb{R}\). Berechnen Sie die Nullstellen von \(h\).
Untersuchen Sie die Monotonie von \(h\).
Berechnen Sie die Koordinaten des Wendepunktes und die Gleichung der Wendetangente \(G_{w}\) von \(G_{h}\).
Die Tangente \(G_{t}\) an \(G_{h}\) im Punkt \(Q(-1;h(1))\) schneidet die Wendetangente im Punkt \(S\). Ermitteln Sie die Koordinaten des Punktes \(S\).
Bestimmen Sie mit Hilfe bisheriger Ergebnisse die Art und die Koordinaten der Extrempunkte von \(G_{h}\) und skizzieren Sie \(G_{h}\), \(G_{w}\) und \(G_{t}\) in ein geeignetes kartesisches Koordinatensystem.
\(G_{h}\), \(G_{w}\) und \(G_{t}\) begrenzen ein endliches Flächenstück. Berechnen Sie Flächenzahl dieser Fläche.
Gegeben ist weiter die Funktion \(k(x)=\frac{29}{72}(x-2)(x-5)(x-8)\) mit \(x\in[2;8]\). Skizzieren Sie einen möglichen Graphen \(G_{k}\) in das Koordinatensystem von Aufgabe (i) ein.
Betrachtet werden die vertikalen Strecken, die entstehen, wenn man einen Punkt \(A\) auf \(G_{h}\) mit einem Punkt \(B\) auf \(G_{k}\) verbindet. Die Punkte \(A\) und \(B\) haben jeweils die gleiche Abszisse. Ermitteln Sie an welcher Stelle die Länge der Strecke \(\overline{AB}\) absolut am größten ist. Berechnen Sie auch die Längenzahl dieser absolut längsten Strecke \(\overline{AB}\).