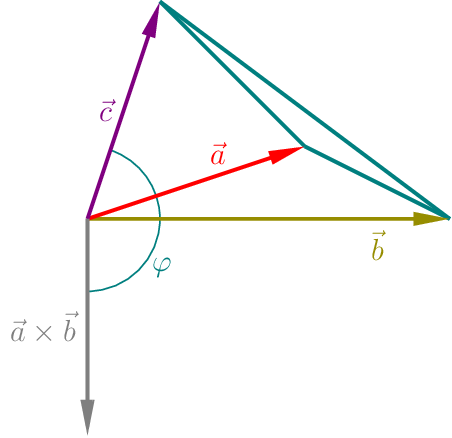
Produkte von Vektoren

• Aufgaben

Das Skalarprodukt

Allgemein gilt:

Für zwei Vektoren \(\vec{a}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}\) und \(\vec{b}=\begin{pmatrix}b_{1}\\ b_{2}\\ b_{3} \end{pmatrix}\) des \(\mathbb{R}^{3}\) heißt die reelle Zahl

\(\vec{a}\cdot\vec{b}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\in\mathbb{R}\)

Skalarprodukt der Vektoren \(\vec{a}\) und \(\vec{b}\).

Für alle \(\vec{a},\vec{b},\vec{c}\in\mathbb{R}^{3}\) und \(\lambda\in\mathbb{R}\) gelten folgende Eigenschaften des Skalarprodukts:

• \(\vec{a}\cdot\vec{b}\in\mathbb{R}\) wird auch kurz \(\vec{a}\vec{b}\in\mathbb{R}\) geschrieben.
• \(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\) (Kommutativgesetz)
• \(\vec{a}(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\) (Distributivgesetz)
• \(\lambda(\vec{a}\cdot\vec{b})=(\lambda\vec{a})\vec{b}=\vec{a}(\lambda\vec{b})\) (Assoziativgesetz)
• \(\vec{a}\cdot\vec{a}=\vec{a}^{2}\)
• \(\vec{a}^{2}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}\cdot\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}=a_{1}^{2}+a_{2}^{2}+a_{3}^{2}\)
• \(\sqrt{\vec{a}^{2}}=\sqrt{\vec{a}\cdot\vec{a}}=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\).
• \(\sqrt{\vec{a}^{2}}\) ist die Länge des Vektors \(\vec{a}\).

---

Der Betrag oder die Längenzahl eines Vektors wird mit \(|\vec{a}|\) oder einfach nur mit \(a\) bezeichnet und es gilt: \(a=|\vec{a}|=\sqrt{\vec{a}^{2}}\).

Für die Längenzahl \(|\overline{AB}|\) einer Strecke \(\overline{AB}\) gilt:

\(|\overline{AB}|=|\overrightarrow{OB}-\overrightarrow{OA}|=|\vec{b}-\vec{a}|=\sqrt{(\vec{b}-\vec{a})^{2}}\).

---

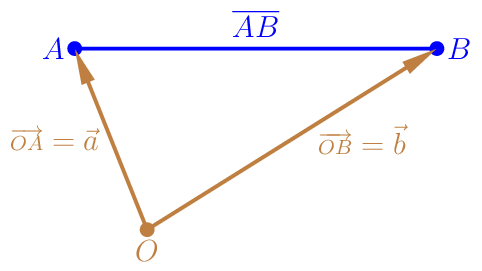
Mit Hilfe des Kosinussatzes im allgemeinen Dreieck können wir eine andere Formel für das Skalarprodukt herleiten.

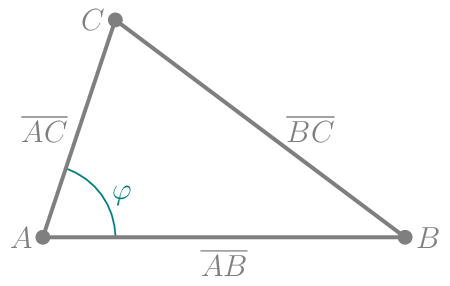
Der Kosinussatz im allgemeinen Dreieck lautet:

\(|\overline{BC}|^{2}=|\overline{AB}|^{2}+|\overline{AC}|^{2}-2\cdot|\overline{AB}|\cdot|\overline{AC}|\cdot\cos\varphi\).

---

Betrachten wir das Gleiche mit Ursprung und Vektoren, so erhalten wir eine Vektorgleichung, die wir geschickt umformen.

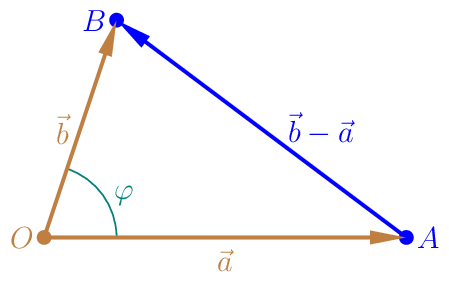
\(|\vec{b}-\vec{a}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2}-2\cdot|\vec{a}|\cdot|\vec{b}|\cdot\cos\varphi\)

\((\vec{b}-\vec{a})^{2}=\vec{a}^{2}+\vec{b}^{2}-2\cdot|\vec{a}|\cdot|\vec{b}|\cdot\cos\varphi\)

\(\vec{b}^{2}-2\cdot\vec{b}\cdot\vec{a}+\vec{a}^{2}=\vec{a}^{2}+\vec{b}^{2}-2\cdot|\vec{a}|\cdot|\vec{b}|\cdot\cos\varphi\)

\(-2\cdot\vec{b}\cdot\vec{a}=-2\cdot|\vec{a}|\cdot|\vec{b}|\cdot\cos\varphi\)

Für das Skalarprodukt erhalten wir:

\(\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos\varphi\).

Stellen wir diese Formel nach \(\varphi\) um, so berechnen wir damit den Winkel \(\varphi=\measuredangle(\vec{a};\vec{b})\), den zwei Vektoren einschließen:

\(\varphi=\measuredangle(\vec{a};\vec{b})=\arccos\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}\cdot|\vec{b}|}\).

Allgemein gilt:

Für den Winkel \(\varphi=\measuredangle(\vec{a};\vec{b})\), den zwei Vektoren \(\vec{a},\vec{b}\in\mathbb{R}^{3}\) einschließen, gilt:

\(\varphi=\measuredangle(\vec{a};\vec{b})=\arccos\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\).

• Für zwei senkrechte Vektoren gilt: \(\vec{a}\perp\vec{b}\Longleftrightarrow\vec{a}\cdot\vec{b}=0\),

• Zwei Vektoren schließen einen spitzen Winkel ein, falls \(\vec{a}\cdot\vec{b}>0\),

• Zwei Vektoren schließen einen stumpfen Winkel ein, falls \(\vec{a}\cdot\vec{b}<0\).

---

Unter einem Einheitsvektor versteht man einen Vektor, der den Betrag \(1\) hat. Den Einheitsvektor, der die gleiche Richtung und die gleiche Orientierung wie ein gegebener geometrischer Vektor \(\vec{a}\) mit \(\vec{a}\neq \vec{0}\) hat, bezeichnen wir mit \(\vec{a}^{\circ}\). Der Vektor \(\vec{a}\) hat die Länge \(a\).

Es gilt also: \(\vec{a}^{\circ}=\frac{1}{a}\cdot\vec{a}\). (Beachte: \(\frac{1}{a}\in\mathbb{R}\))

---

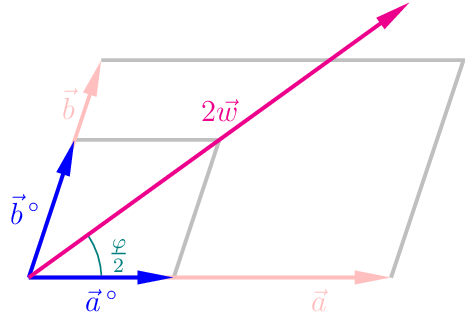
Die Diagonale der Raute, die durch \(\vec{a}^{\circ}\) und \(\vec{b}^{\circ}\) bestimmt wird, halbiert den Winkel \(\varphi=\measuredangle(\vec{a};\vec{b})\) zwischen \(\vec{a}\) und \(\vec{b}\). Setzt man \(\vec{w}=\vec{a}^{\circ}+\vec{b}^{\circ}\), dann ist jeder Vektor der Form \(\lambda \cdot \vec{w}\) mit \(\lambda \in\mathbb{R}^{+}\) ein Vektor, der den Winkel \(\varphi\) halbiert.

Das Vektorprodukt

Allgemein gilt:

Für alle \(\vec{a}=\begin{pmatrix}a_{1}\\ a_{2}\\ a_{3} \end{pmatrix}\) und \(\vec{b}=\begin{pmatrix}b_{1}\\ b_{2}\\ b_{3} \end{pmatrix}\) des \(\mathbb{R}^{3}\) heißt der Vektor

\(\vec{a}\times\vec{b}=\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\ a_{3}b_{1}-a_{1}b_{3}\\ a_{1}b_{2}-a_{2}b_{1} \end{pmatrix}\) das Vektorprodukt der Vektoren \(\vec{a}\) und \(\vec{b}\).

Für alle \(\vec{a},\vec{b},\vec{c}\in\mathbb{R}^{3}\) verschieden vom Nullvektor und \(\lambda\in\mathbb{R}\) gelten folgende Eigenschaften des Vektorprodukts:

• \(\vec{a}\times\vec{b}\) ist ein Vektor, also \(\vec{a}\times\vec{b}\in\mathbb{R}^{3}\).
• \(\vec{a}\times\vec{b}\) steht senkrecht auf \(\vec{a}\) und \(\vec{b}\), also \(\vec{a}\times\vec{b}\perp\vec{a}\) und \(\vec{a}\times\vec{b}\perp\vec{b}\).
• Die Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{a}\times\vec{b}\) bilden in dieser Reihenfolge ein Rechtssystem (rechte Hand Regel).

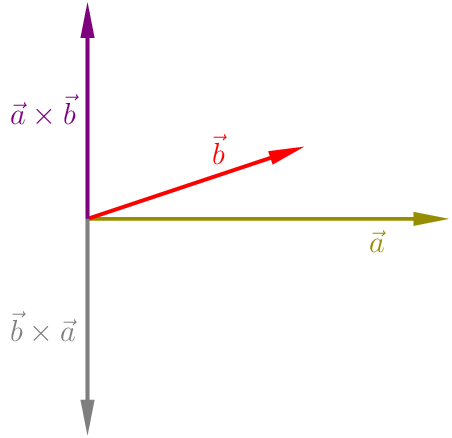
• Alternativgesetz: \(\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}\).
• Distributivgesetz: \(\vec{a}\times(\vec{b}+\vec{c})=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}\)
• gemischtes Assoziativgesetz: \(\lambda\vec{a}\times\vec{b}=\lambda(\vec{a}\times\vec{b})=\vec{a}\times\lambda\vec{b}\)
• Das reine Assoziativgesetz gilt im Allgemeinen nicht: \((\vec{a}\times\vec{b})\times\vec{c}\neq\vec{a}\times(\vec{b}\times\vec{c})\).
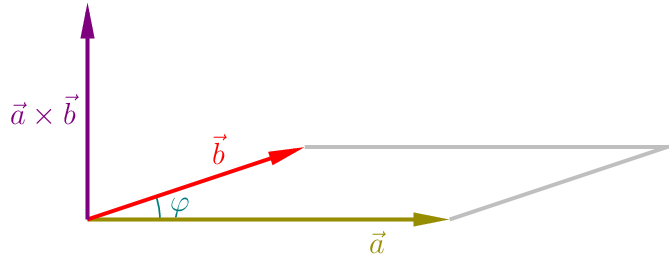
• Geometrische Bedeutung des Vektorproduktes: Ist \(\varphi=\measuredangle(\vec{a};\vec{b})\) der Winkel zwischen \(\vec{a}\) und \(\vec{b}\), so ist der Betrag von \(\vec{a}\times\vec{b}\) gleich der Flächenzahl des von \(\vec{a}\) und \(\vec{b}\) bestimmten Parallelogramms:
  \(|\vec{a}\times\vec{b}|=|\vec{a}|\cdot|\vec{b}|\cdot\sin\varphi\).

Das Spatprodukt

Ein Spat, auch Parallelflach genannt, wird von einer Ecke ausgehend, von drei Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) des \(\mathbb{R}^{3}\) bestimmt.

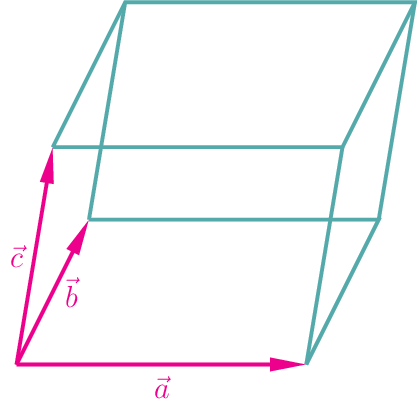
Die Maßzahl des Volumens des Spats, also die Volumenzahl \(V\), berechnen wir mit der Formel:

\(V=|(\vec{a}\times\vec{b})\cdot\vec{c}|\).

Allgemein gilt:

Die reelle Zahl

\((\vec{a}\times\vec{b})\cdot\vec{c}\in\mathbb{R}\)

ist das Spatprodukt der Vektoren \(\vec{a},\vec{b},\vec{c}\in\mathbb{R}^{3}\).

Das Spatprodukt hat folgende Eigenschaften:

• Das Spatprodukt ist eine reelle Zahl: \((\vec{a}\times\vec{b})\cdot\vec{c}\in\mathbb{R}\).
• Der Betrag \(|(\vec{a}\times\vec{b})\cdot\vec{c}|\) des Spatprodukts \(\left( \vec{a}\times \vec{b}\right) \cdot \vec{c}\) ist die Maßzahl des Volumens des von \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) bestimmten Spats.
• ist \((\vec{a}\times\vec{b})\cdot\vec{c} = 0\), so liegen die Vektoren \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) in einer Ebene. Man sagt, die drei Vektoren sind komplanar oder sie sind linear abhängig. Ansonsten sind die drei Vektoren linear unabhängig.
• Eine Pyramide mit einem Parallelogramm als Grundfläche hat die Volumenmaßzahl
  \(V=\frac{1}{3}|(\vec{a}\times\vec{b})\cdot\vec{c}|\).
  In der Skizze ist der Winkel \(\varphi\), den die Vektoren \(\vec{a}\times\vec{b}\) und \(\vec{c}\) bilden, ein spitzer Winkel .

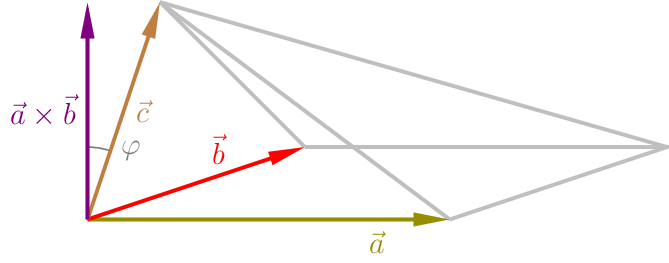
• Eine Pyramide mit einem Dreieck als Grundfläche hat die Volumenmaßzahl
  \(V=\frac{1}{6}|(\vec{a}\times\vec{b})\cdot\vec{c}|\).
  In der Skizze ist der Winkel \(\varphi\), den die Vektoren \(\vec{a}\times\vec{b}\) und \(\vec{c}\) bilden, ein stumpfer Winkel .