Zufallsgrößen

• Aufgaben

Auf Glücksspiele aller Art treffen wir in unserem alltäglichen Leben recht häufig, z.B. Sportwetten, Lotto oder Ziehen von Lose bei der Tombola. Grundlage bei all diesen Spielen sind Zufallsexperimente. Jedem Ergebnis des Zufallsexperiments ordnet man einen Zahlenwert zu, der positiv, negativ oder gleich Null sein kann. Diese Zahlenwerte entsprechen Geldbeträgen, die über Gewinn oder Verlust beim Glücksspiel entscheiden.

Beispiel 1

Auf dem Volksfest an einem unbekannten Ort, läuft an der Bude eines Glücksspielbetreibers ein Spiel nach dem Motto „Du bekommst immer was zurück!“. Bei diesem Spiel wirft ein Spieler eine Laplace-Münze drei Mal. Der Einsatz für jedes Spiel liegt bei \(5\,\text{€}\) und es gelten folgende Spielregeln:

• fällt dreimal Kopf, so bekommt der Spieler \(10\,\text{€}\) vom Betreiber,

• fällt zweimal Kopf, so bekommt der Spieler \(5\,\text{€}\) vom Betreiber,

• fällt einmal Kopf, so bekommt der Spieler \(3\,\text{€}\) zurück,

• fällt nur Wappen, so bekommt der Spieler \(2\,\text{€}\) zurück.

Ist dieses Spiel fair?

---

Um eine Antwort auf diese Frage geben zu können, führen wir einige bekannte, aber auch neue Berechnungen durch.

1. Bestimmen Sie für das gegebene Zufallsexperiment die Wahrscheinlichkeiten aller Elementarereignisse mit Hilfe eines Baumdiagramms und ordnen Sie jedem Elementarereignis den Geldbetrag zu, den ein Spieler gewinnt oder verliert.

2. Geben Sie in Worten an, was hier die Zufallsgröße ist und fassen Sie alle Zufallswerte dieser Experiments in Mengenschreibweise zusammen.

3. Erstellen Sie die Wahrscheinlichkeitsverteilung des Experiments in Tabellenform und veranschaulichen Sie diese Wahrscheinlichkeitsverteilung mit einem Stabdiagramm und einem Histogramm.

4. Berechnen Sie den Erwartungswert der Wahrscheinlichkeitsverteilung und geben Sie in Worten die Bedeutung des Erwartungswertes an. Beurteilen sie zu guter Letzt, ob dieses Glücksspiel für einen Spieler fair ist.

---

Aufgabe (a)

Bestimmen Sie für das gegebene Zufallsexperiment die Wahrscheinlichkeiten aller Elementarereignisse mit Hilfe eines Baumdiagramms und ordnen Sie jedem Elementarereignis den Geldbetrag zu, den ein Spieler gewinnt oder verliert.

---

Baumdiagramm

---

Die Wahrscheinlichkeiten aller Elementarereignisse fassen wir in einer Tabelle zusammen. In einer dritten Zeile geben wir den Gewinn oder Verlust, der dem jeweiligen Ergebnis entspricht, an.

\(\omega\)	KKK	KKW	KWK	KWW	WKK	WKW	WWK	WWW
\(P(\omega)\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)	\(\small{0.125}\)
\(z\)	\(\;\small{5}\)	\(\;\small{0}\)	\(\;\small{0}\)	\(\;\small{-2}\)	\(\;\small{0}\)	\(\;\small{-2}\)	\(\;\small{-2}\)	\(\;\small{-3}\)

Allgemein gilt:

Wird jedem Ergebnis eines Zufallsexperiments eindeutig eine Zahl zugeordnet, so heißt diese Zahl Zufallswert. Zufallswerte werden mit kleinen Buchstaben bezeichnet, z.B. z, t, x.

Aufgabe (b)

Geben Sie in Worten an, was hier die Zufallsgröße ist und fassen Sie alle Zufallswerte dieser Experiments in Mengenschreibweise zusammen.

---

Die Tabelle zeigt, dass jedem Ergebnis des Zufallsexperiments eindeutig eine Zahl zugeordnet ist. Da es sich um eine eindeutige Zuordnung handelt, definieren wir eine Funktion, die jedem Ergebnis des Zufallsexperiments eindeutig eine Zahl zuordnet. So eine Funktion nennen wir Zufallsgröße.

Allgemein gilt:

Eine Funktion \(X\), deren Definitionsmenge der Ergebnisraum

\(\Omega=\left\{ \omega _{1},\omega _{2},\ldots ,\omega _{n}\right\}\)

eines Zufallsexperiments und deren Wertemenge eine Menge reeller Zahlen ist, heißt Zufallsgröße des Experiments.

Die Funktionswerte \(X(\omega _{k})\) sind die reellen Zahlen, die durch die Funktion \(X\) den Ergebnissen \(\omega _{k}\) von \(\Omega\) zugeordnet wurden. Das sind die Zufallswerte des Experiments.

Man schreibt dazu: \(X(\omega _{k})=x_{k}\) oder kurz \(X=x_{k}\).

In unserer Aufgabe ist die Zufallsgröße \(Z\) eine Funktion, die jedem Ergebnis des Zufallsexperiments den Gewinn oder Verlust zuordnet, den ein Spieler erzielt. Die Definitionsmenge von \(Z\) ist der Ergebnisraum \(\Omega\) und die Wertemenge ist \(W_{Z}=\{-3;-2;0;5\}\).

Aufgabe (c)

Erstellen Sie die Wahrscheinlichkeitsverteilung des Experiments in Tabellenform und veranschaulichen Sie diese Wahrscheinlichkeitsverteilung mit einem Stabdiagramm und einem Histogramm.

---

Betrachten wir die obige Tabelle, so stellen wir fest, dass es Ergebnisse des Zufallsexperiments gibt, die den gleichen Zufallswert zugeordnet bekommen haben. Damit erstellen wir eine neue Tabelle, aus der wir die Wahrscheinlichkeit mit der ein Zufallswert eintritt, entnehmen können. Diese Tabelle heißt Wahrscheinlichkeitsverteilung der Zufallsgröße \(Z\).

\(z\)	\(\;\small{-3}\)	\(\;\small{-2}\)	\(\;\small{0}\)	\(\;\small{5}\)
\(P(Z=z)\)	\(\small{0.125}\)	\(\small{0.375}\)	\(\small{0.375}\)	\(\small{0.125}\)

Allgemein gilt:

Bei einer vollständigen Wahrscheinlichkeitsverteilung ist die Summe der Wahrscheinlichkeiten \(P(X=x_{k})\) stets gleich \(1\).

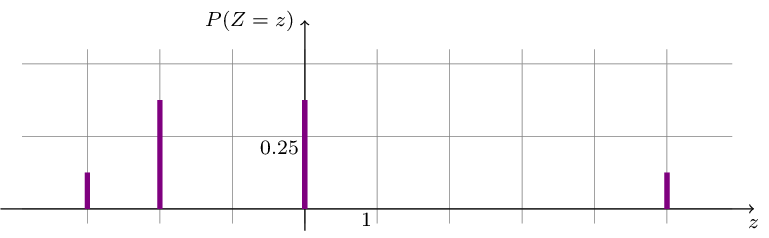
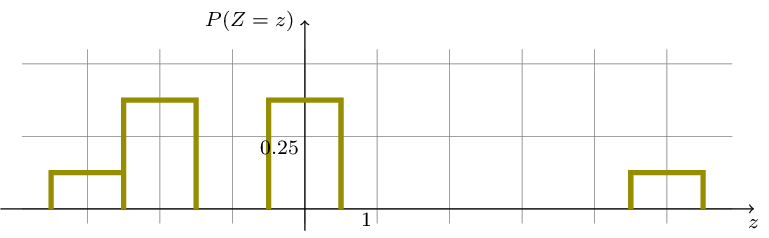
Die Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\) stellen wir auch graphisch dar. Dazu verwenden wir ein Stabdiagramm oder ein Histogramm.

Darstellung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(Z\) mit einem Stabdiagramm:

---

Darstellung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(Z\) mit einem Histogramm:

Aufgabe (d)

Berechnen Sie den Erwartungswert der Wahrscheinlichkeitsverteilung und geben Sie in Worten die Bedeutung des Erwartungswertes an. Beurteilen sie zu guter Letzt, ob dieses Glücksspiel für einen Spieler fair ist.

---

Spielt ein Spieler dieses Spiel, so weiß er, dass er beim Ergebnis \(\{KKK\}\) recht viel gewinnt, ansonsten aber Verluste hinnehmen muss. Es wäre interessant zu wissen, wie die Gewinnchancen stehen, wenn man das Spiel sehr oft spielt. Das kann man auch wirklich tun, man spielt sehr viele Spiele und bilanziert dann über Gewinn oder Verlust. Besser und weniger zeitaufwändig wäre es aber, wenn wir die Gewinnchancen mit Hilfe einer Formel schon im voraus berechnen könnten.

Aus der Wahrscheinlichkeitsverteilung ist es möglich die durchschnittlichen Gewinnchancen zu ermitteln.

\(z\)	\(\;\small{-3}\)	\(\;\small{-2}\)	\(\;\small{0}\)	\(\;\small{5}\)
\(P(Z=z)\)	\(\small{0.125}\)	\(\small{0.375}\)	\(\small{0.375}\)	\(\small{0.125}\)

---

Den durchschnittlichen Gewinn oder Verlust ermitteln wir, indem wir jeden Zufallswert mit seiner Wahrscheinlichkeit multiplizieren und alle Produkte addieren. Der ausgerechnete Wert ist der Ertwartungswert der Zufallsgröße \(Z\).

\(E(Z)=5\cdot 0.125+0\cdot0.375-2\cdot 0.375-3\cdot 0.125=-0.5\)

Das bedeutet, dass ein Spieler bei vielem Spielen bei jedem Spiel \(0.5\) € pro Spiel verliert. Somit sagen wir, dass dieses Spiel für einen Spieler nicht fair ist.

Allgemein gilt:

Der Erwartungswert einer Zufallsgröße \(X\) berechnen wir, indem wir jeden Zufallswert mit seiner Wahrscheinlichkeit multiplizieren und alle Produkte addieren.

Wir bezeichnen den Erwartungswert mit \(E(X)\) oder den griechischen Buchstaben \(\mu\) (mü).

\(E(X)=x_{1}\cdot P(X=x_{1})+x_{2}\cdot P\left( X=x_{2}\right) +\ldots+x_{k}\cdot P(X=x_{k})\)

\(E(X)=\sum\limits_{i=1}^{k}x_{i}\cdot P(X=x_{i})\)

Beispiel 2

Wir betrachten die Wahrscheinlichkeitsverteilungen zweier unterschiedlicher Zufallsgrößen \(Z\) und \(T\).

\(z\)	\(\;\small{-1}\)	\(\;\small{0}\)	\(\;\small{1}\)	\(\;\small{2}\)	\(\;\small{3}\)	\(\;\small{4}\)
\(P(Z=z)\)	\(\small{\frac{1}{14}}\)	\(\small{\frac{2}{14}}\)	\(\small{\frac{2}{14}}\)	\(\small{\frac{3}{14}}\)	\(\small{\frac{3}{14}}\)	\(\small{\frac{3}{14}}\)

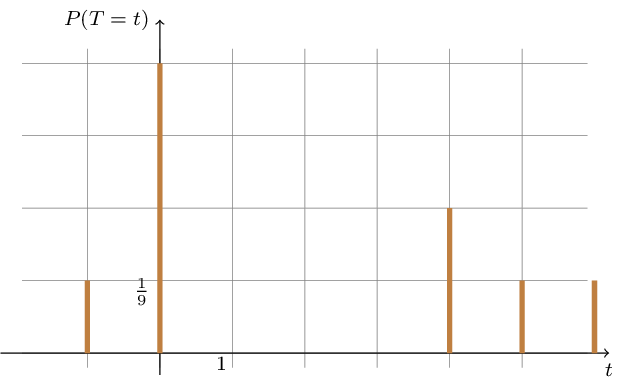
\(t\)	\(\;\small{-1}\)	\(\;\small{0}\)	\(\;\small{4}\)	\(\;\small{5}\)	\(\;\small{6}\)
\(P(T=t)\)	\(\small{\frac{1}{9}}\)	\(\small{\frac{4}{9}}\)	\(\small{\frac{2}{9}}\)	\(\small{\frac{1}{9}}\)	\(\small{\frac{1}{9}}\)

1. Untersuchen Sie, ob tatsächlich zwei Wahrscheinlichkeitsverteilungen vorliegen.

2. Berechnen Sie die Erwartungswerte von \(Z\) und \(T\).

3. Stellen sie \(Z\) und \(T\) in einem Stabdiagramm graphisch dar und tragen Sie \(E(Z)\) und math:E(T) als senkrechte Geraden in die Diagramme ein.

4. Nehmen Sie für beide Diagramme Stellung zur Streuung der Zufallswerte um den jeweiligen Erwartungswert.

Aufgabe (a)

Untersuchen Sie, ob tatsächlich zwei Wahrscheinlichkeitsverteilungen vorliegen.

In beiden Diagrammen liegen die Wahrscheinlichkeiten zwischen \(0\) und \(1\) und die Summe der Wahrscheinlichkeiten ist genau \(1\), also stellen beide Tabellen jeweils eine Wahrscheinlichkeitsverteilung dar.

Aufgabe (b)

Berechnen Sie die Erwartungswerte von \(Z\) und \(T\).

\(E(Z)=-\frac{1}{14}+0\cdot\frac{2}{14}+\frac{2}{14}+2\cdot\frac{3}{14}+3\cdot\frac{3}{14}+4\cdot\frac{3}{14}\)

\(E(Z)=2\)

\(E(T)=-\frac{1}{9}+0\cdot\frac{4}{9}+4\cdot\frac{2}{9}+5\cdot\frac{1}{9}+6\cdot\frac{1}{9}\)

\(E(T)=2\)

Aufgabe (c)

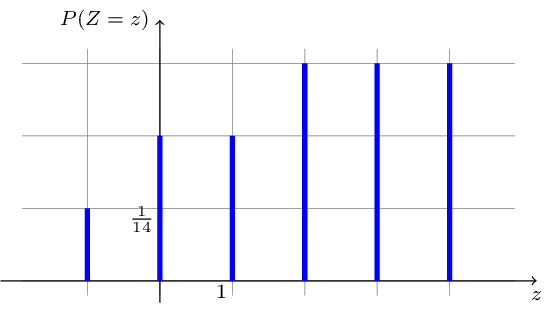
Darstellung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(Z\) mit einem Stabdiagramm:

---

Darstellung der Wahrscheinlichkeitsverteilung der Zufallsgröße \(T\) mit einem Stabdiagramm:

Aufgabe (d)

Nehmen Sie für beide Diagramme Stellung zur Streuung der Zufallswerte um den jeweiligen Erwartungswert.

Obwohl die Diagramme unterschiedlich aussehen, gilt \(E(Z)=E(T)=2\). Die Streuung der Zufallswerte um den Erwartungswert ist bei der Zufallsgröße \(Z\) eindeutig kleiner, als bei Zufallsgröße \(T\).

---

Das bedeutet, dass der Erwartungswert allein nicht ausreicht, um eine Zufallsgröße zu charakterisieren.Man braucht ein Maß dafür, wie weit die Zufallswerte um ihren Erwartungswert nach links oder rechts streuen. Um diesen Unterschied zahlenmäßig zu erfassen berechnen wir für jeden Zufallswert das Quadrat aus der Differenz zwischen Zufallswert und Erwartungswert. Diese neu berechneten Werte setzen wir in die Formel zur Berechnung des Erwartungswertes ein und erhalten eine neu Größe, nämlich die Varianz der Zufallsgröße.

Für die Zufallsgrößen \(Z\) und \(T\) berechnen wir nun die Varianz.

\(Var(Z)=(-1-2)^{2}\cdot\frac{1}{14}+(0-2)^{2}\cdot\frac{2}{14}+(1-2)^{2}\cdot\frac{2}{14}\)

\(\qquad\qquad+(2-2)^{2}\cdot\frac{3}{14}+(3-2)^{2}\cdot\frac{3}{14}+(4-2)^{2}\cdot\frac{3}{14}\)

\(Var(Z)=\frac{34}{14}\approx 2.43\)

\(Var(T)=(-1-2)^{2}\cdot\frac{1}{9}+(0-2)^{2}\cdot\frac{4}{9}+(4-2)^{2}\cdot\frac{2}{9}\)

\(\qquad\qquad+(5-2)^{2}\cdot\frac{1}{9}+(6-2)^{2}\cdot\frac{1}{9}\)

\(Var(T)=\frac{58}{9}\approx 6.44\)

---

Da wir bei der Berechnung der Varianz quadriert haben muss an einer anderen Stelle die Wurzel gezogen werden. Das machen wir nachdem die Varianz berechnet wurde. Wir erhalten eine neue Größe, nämlich die Standardabweichung, die wir mit dem griechischen Buchstabe \(\sigma\) (sigma) bezeichnen. Die Standardabweichung ist ein Maß für die Streuung der Zufallswerte um den Erwartungswert.

In unserem Beispiel berechnen wir die Standardabweichung mit:

\(\sigma=\sqrt{2.43}\approx 1.56\) und

\(\sigma=\sqrt{6.44}\approx 2.54\).

Allgemein gilt:

Sei \(X\) eine Zufallsgröße mit der Wertemenge \(W_{X}=\left\{x_{1},x_{2},\ldots ,x_{k}\right\}\) und \(E(X)=\mu\) der Erwartungswert von \(X\).

Dann berechnen wir die Varianz mit: \(Var(X)=E\left( \left( X-\mu \right) ^{2}\right)=\sum\limits_{i=1}^{k}\left( x_{i}-\mu \right) ^{2}\cdot P\left(X=x_{i}\right)\).

Man schreibt statt \(Var(X)\) oft auch \(\sigma ^{2}\).

Als Standardabweichung der Zufallsgröße \(X\) bezeichnet man die Zahl \(\sigma=\sqrt{Var\left( X\right) }\).

Die Varianz \(Var(X)\) einer Zufallsgröße \(X\) kann auch mit Hilfe der Verschiebungsformel berechnet werden:

\(\sigma ^{2}=E\left( X^{2}\right) -\mu ^{2}\).