Prüfung 2024

Analysis, Teil 1

Aufgabe 1

Gegeben ist die quadratische Funktion $p:x\mapsto -x^2+1$ mit $x\in \mathbb{R}$. Den Graphen von $p$ bezeichnen wir $G_p$. $G_p$ und die $x$-Achse schließen ein endliches Flächenstück ein. Berechnen Sie die Flächenzahl $A$ dieses Flächenstücks. [4]

---

Tipp

Die Nullstellen von $p$ sind die Integrationsgrenzen.

Ergebnis

$A=\frac{4}{3}$

Aufgabe 2

Gegeben ist die Funktion $k:x\mapsto 0.5(x-3{)}^2(2x+\frac{4}{3})$ mit $x\in \mathbb{R}$.

Aufgabe (a)

Geben Sie die Nullstellen der Funktion $k$ mit ihrer jeweiligen Vielfachheit an und bestimmen Sie damit ein Intervall, in dem die $x$-Koordinate des lokalen Hochpunkts des Graphen der Funktion $k$ liegt. [4]

---

Tipp

Wir erstellen eine Vorzeichentabelle von $k(x)$.

Ergebnis

$I=]-\frac{2}{3};3[$

Aufgabe (b)

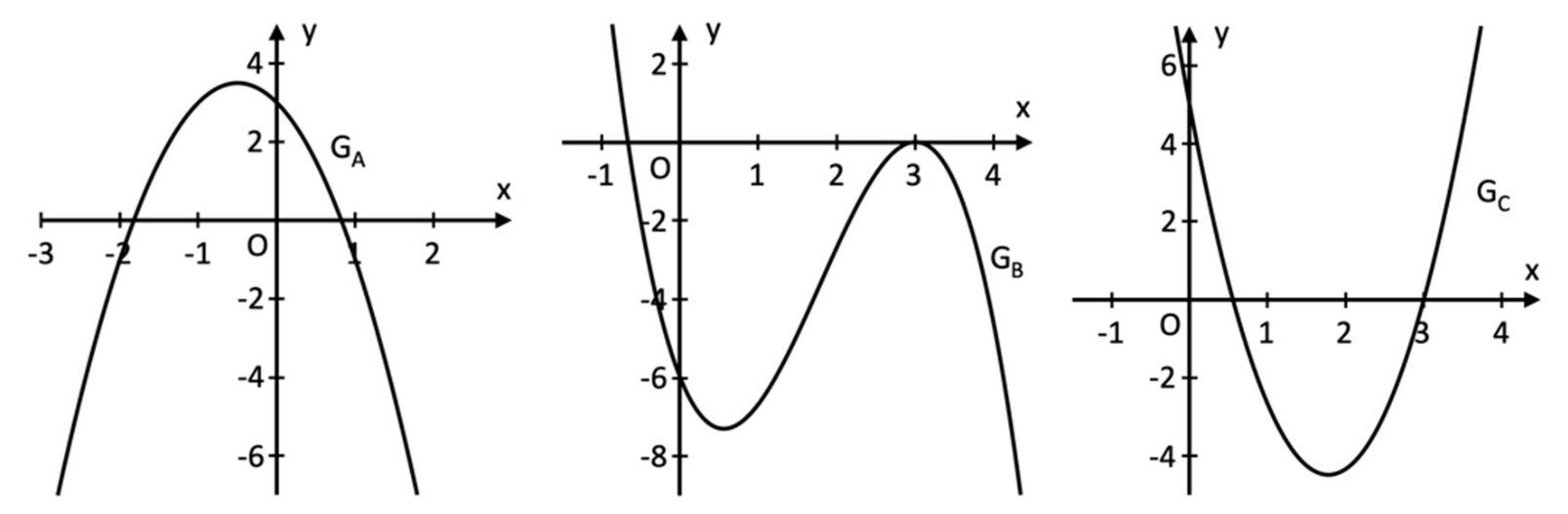
In der nachfolgenden Abbildung sind Ausschnitte der Graphen $G_A$ , $G_B$ und $G_C$ von in ganz $\mathbb{R}$ definierten Funktionen dargestellt. Entscheiden Sie begründet, welcher der drei Graphen $G_A$ , $G_B$ und $G_C$ zur Ableitungsfunktion von $k$ gehört. [3]

Tipp

• Wir betrachten die Stelle $x=3$.

Aufgabe 3

Gegeben sind die Funktionen $g$ und $h$ durch die Funktionsgleichungen $g(x)=2\cdot e^x-1$ und $h(x)=e^{2x}$ mit $x\in \mathbb{R}$.

Aufgabe (a)

Bestimmen Sie rechnerisch die Koordinaten des einzigen gemeinsamen Punktes $P$ der Graphen der beiden Funktionen $g$ und $h$. [4]

---

Tipp

Wir verwenden die Substitution.

Ergebnis

$P(0;1)$

Aufgabe (b)

Der Graph der Funktion $g$ wird an der $x$-Achse gespiegelt und anschließend um zwei Einheiten entlang der $y$-Achse nach oben verschoben. Der daraus entstandene neue Funktionsgraph gehört zur Funktion $j$. Geben Sie einen Funktionsterm der Funktion $j$ an. [2]

---

Tipp

• Wir spiegeln an der $x$-Achse und verschieben entlang der $y$-Achse.

Aufgabe 4

Die folgende Abbildung zeigt einen Ausschnitt des Graphen $G_{f^{\prime }}$ der Ableitungsfunktion $f^{\prime }$ einer auf $\mathbb{R}$ definierten ganzrationalen Funktion $f$ vierten Grades. Die Funktion $F$ bezeichnet eine Stammfunktion von $f$ .

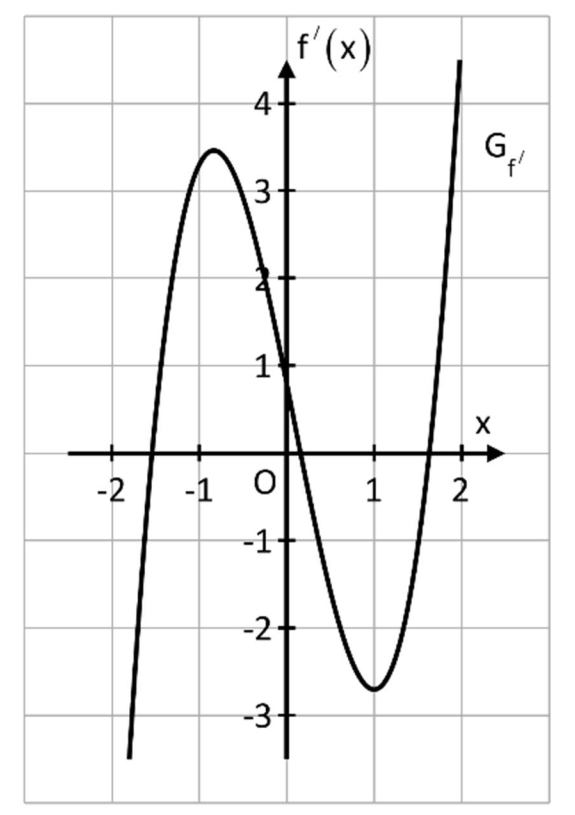
Entscheiden Sie jeweils, ob folgende Aussagen wahr (w) oder falsch (f) sind bzw. ob dies mit den gegebenen Informationen nicht entschieden (n) werden kann. [5]

1. $G_f$ ist punktsymmetrisch zum Ursprung.

2. $G_f$ besitzt genau zwei Wendepunkte.

3. $G_f$ besitzt einen globalen Tiefpunkt.

4. F hat genau vier Nullstellen.

5. Für $x\to -\mathrm{\infty }$ gilt: $f(x)\to +\mathrm{\infty }$.

---

Tipp

• Wenn $G_{f^{\prime }}$ weder zum Urprung noch zur $y$-Achse symmetrisch ist, dann ist $G_f$ auch nicht zum Ursprung oder $y$-Achse symmetrisch.

• Wir notieren das Monotonieverhalten von $G_f$ .

Stochastik, Teil 1

Im Folgenden werden relative Häufigkeiten als Wahrscheinlichkeiten interpretiert.

Aufgabe 1

Bei der Befragung von zufällig ausgewählten Kunden eines Lebensmittelmarkts wird unter anderem untersucht, ob sie Vegetarier (V) sind bzw. ob sie in bar (B) bezahlen. Das Ergebnis der Befragung ist in folgender Vierfeldertafel dargestellt. Untersuchen Sie, ob der Anteil der Barzahler unter den Vegetariern höher ist als der Anteil der Barzahler unter den Nicht-Vegetariern. [3]

	$V$	$\bar{V}$
$B$	$0.10$	$0.45$	$0.55$
$\bar{B}$	$0.05$	$0.40$	$0.45$
	$0.15$	$0.85$	$1$

Aufgabe 2

Die durchgeführte Umfrage hat ebenfalls ergeben, dass $80\mathrm{\%}$ aller Befragten beim Einkaufen im Supermarkt eine eigene Einkaufstasche dabei haben. Betrachtet werden nun hintereinander anstehende Kunden an einer Supermarktkasse. Geben Sie für die nachfolgenden Ereignisse jeweils einen Term an, der die Berechnung der Wahrscheinlichkeit für das beschriebene Ereignis ermöglicht. [2]

$E_1:$ „Von zehn Kunden haben genau vier eine eigene Einkaufstasche mitgebracht.“

$E_2:$ „Von acht Kunden kaufen nur genau die ersten zwei und der letzte Kunde ohne eigene Einkaufstasche ein.“

Aufgabe 3

Ein zufällig ausgewählter Kunde nutzt unabhängig davon, ob er eine Einkaufstasche dabei hat oder nicht, mit der Wahrscheinlichkeit $p$ einen Einkaufswagen. Die Wahrscheinlichkeit dafür, dass von zwei Kunden, die nacheinander den Supermarkt betreten, genau einer einen Einkaufswagen nutzt, beträgt $32\mathrm{\%}$ . Geben Sie den Ansatz zur Berechnung der Wahrscheinlichkeit $p$ an. Die Berechnung von $p$ ist nicht erforderlich. [2]

---

Tipp

• Für die beschriebene Situation gibt es genau zwei Möglichkeiten und die beschriebene Situation tritt mit einer Wahrscheinlichkeit von $0.32$ ein.

Aufgabe 4

Im Supermarkt befinden sich insgesamt drei Kassen. Die Zufallsgröße $X$ beschreibt die Anzahl der gleichzeitig besetzten Kassen während der Öffnungszeiten. Die folgende Tabelle zeigt die vollständige Wahrscheinlichkeitsverteilung von $X$.

$x$	$0$	$1$	$2$	$3$
$P(X=x)$	$0.05$	$0.45$	$0.35$	$0.15$

Aufgabe (a)

Bestimmen Sie den Erwartungswert der Zufallsgröße $X$ und interpretieren Sie den Wert im beschriebenen Sachzusammenhang. [2]

Aufgabe (b)

Die Varianz der Zufallsgröße $X$ hat den Wert $0.64$. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Werte der Zufallsgröße $X$ innerhalb der einfachen Standardabweichung um ihren Erwartungswert liegen. [3]

Analysis, Teil 2.1

Aufgabe 1

Gegeben ist die Funktion $f:x\mapsto -\frac{1}{2}{x}^4-2x^3-2x^2$ mit $x\in \mathbb{R}$. Der Graph der Funktion $f$ in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.

Aufgabe (a)

Berechnen Sie die Nullstellen der Funktion $f$. [3]

Aufgabe (b)

Ermitteln Sie jeweils die Art und die Koordinaten aller Punkte, in denen $G_f$ eine waagrechte Tangente besitzt. [7]

---

Tipp

• Wir berechnen die Nullstellen der ersten Ableitung.

Aufgabe (c)

Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen $G_f$ für $-3\le x\le 1$ in ein kartesisches Koordinatensystem. [4]

Aufgabe (d)

Der Graph $G_p$ einer quadratischen Funktion $p$ mit $x\in \mathbb{R}$ besitzt in einem kartesischen Koordinatensystem den Scheitelpunkt $S(-1;-1.5)$ und schneidet den Graphen $G_f$ in den Punkten $A(-3;-4.5)$ und $B(1;-4.5)$.

1. Bestimmen Sie einen Funktionsterm von $p$ und zeichnen Sie die zugehörige Parabel für $-3\le x\le 1$ in das vorhandene Koordinatensystem ein. [6]

---

Tipp

Wir verwenden zur Bestimmung des Terms $p(x)$ die Scheitelform der quadratischen Funktion.

Ergebnis

$p(x)=\frac{3}{4}{x}^2-\frac{3}{2}x-\frac{9}{4}$

2. Die beiden Graphen $G_f$ und $G_p$ schließen ein endliches Flächenstück ein. Berechnen Sie die exakte Maßzahl des Flächeninhalts des beschriebenen Flächenstücks. [4]

---

Tipp

• Die Integrationsgrenzen verwenden wir aus den Angaben von vorherigen Aufgaben.

• Vor der Integration bestimmen wir den Term $f(x)-p(x)$.

Ergebnis

$A=\frac{104}{15}$

Aufgabe 2

In sogenannten Aluminiumhütten wird nach einem bestimmten Verfahren Aluminium aus Aluminiumoxid gewonnen. Die Temperatur vom Ausgangsstoff bis zum fertigen Endprodukt Aluminium während des Herstellungsprozesses kann modellhaft durch die Funktion $T$ mit der Funktionsgleichung $T(t)=250\cdot t\cdot e^{-0.1\cdot t}+22$ mit $t\ge 0$ beschrieben werden. Dabei steht die Variable $t$ für die Zeit in Minuten ab dem Zeitpunkt $t_0=0$ . Der Funktionswert von $T$ gibt die Temperatur in Grad Celsius zum Zeitpunkt $t$ an. Auf das Mitführen von Einheiten während der Rechnungen wird verzichtet. Runden Sie Ihre Ergebnisse sinnvoll.

Aufgabe (a)

Berechnen Sie die Temperatur im Herstellungsprozess nach fünf Minuten und die Temperatur, welche sich nach diesem Modell theoretisch langfristig einstellt. [4]

Aufgabe (b)

Beim Erreichen des Temperaturmaximums liegt Aluminium in flüssiger Form vor. Es wird mittels eines Saugrohres abgesaugt und kühlt anschließend ab. Ermitteln Sie rechnerisch dieses Temperaturmaximum. [7]

---

Tipp

• Wir berechnen die Koordinaten des absolut höchsten Punktes des Graphen von $T$.

• Zusätzlich dazu betrachten wir auch das Verhalten von $T(t)$ an den Rändern des Definitionsbereichs.

Ergebnis

$T(10)\approx 941.70{}^{\circ }\mathrm{C}$

Aufgabe (c)

Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen der Funktion $T$ im Bereich $0\le t\le 60$ in ein Koordinatensystem. Wählen Sie dazu für beide Achsen einen geeigneten Maßstab. Entnehmen Sie anschließend dem Graphen den Zeitpunkt $t_{20-fach}$ , zu dem die Temperatur im Abkühlvorgang dem $20$-fachen der Anfangstemperatur entspricht. [5]

Aufgabe (d)

Für die Koordinaten des Wendepunktes des Graphen der Funktion $T$ gilt ohne Nachweis $W(20;T(20))$. Berechnen Sie $\dot{T}(20)$ und interpretieren Sie den Wert im Sinne der vorliegenden Thematik. [3]

Analysis, Teil 2.2

Aufgabe 1

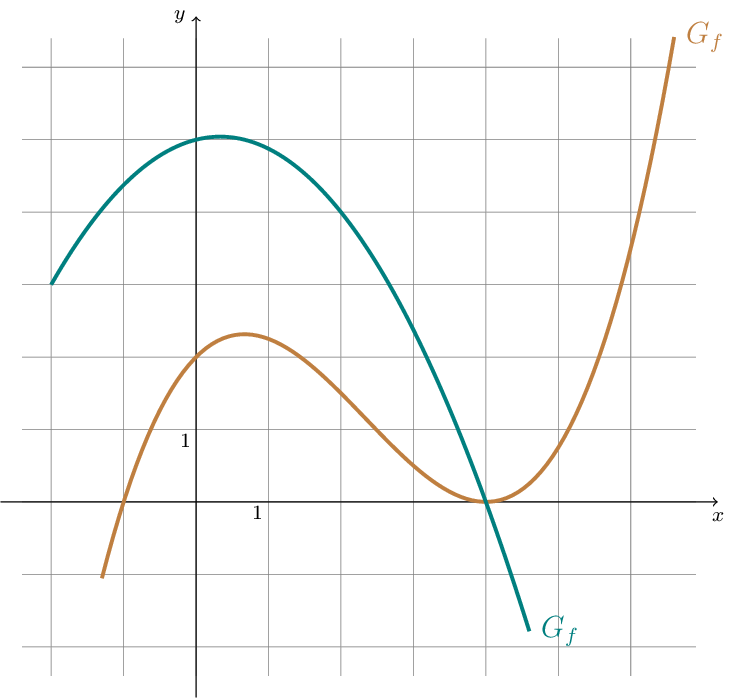
Die Abbildung zeigt ausschnittsweise den Graphen $G_f$ einer ganzrationalen Funktion $f$ dritten Grades mit $x\in \mathbb{R}$ und den Graphen $G_p$ der quadratischen Funktion $p:x\mapsto -\frac{3}{8}{x}^2+\frac{1}{4}x+5$ mit $x\in \mathbb{R}$ .

Aufgabe (a)

Entnehmen Sie der Abbildung geeignete ganzzahlige Werte und bestimmen Sie einen Funktionsterm $f(x)$ der Funktion $f$ . [3]

---

Tipp

• Wir geben den Term $f(x)$ zerlegt in Linearfaktoren an.

Aufgabe (b)

Die Funktion $f$ lässt sich auch in der Form $f(x)=\frac{1}{8}(x^3-7x^2+8x+16)$ darstellen. Der Nachweis hierfür ist nicht erforderlich.

1. Bestimmen Sie eine Gleichung der Tangente $G_g$ an $G_f$ im Punkt $P(0;2)$. [3]

---

Tipp

Die Tangente hat die Steigung $f^{\prime }(0)$ .

Ergebnis

g(x)=x+2

2. Zeigen Sie, dass in keinem Punkt des Graphen $G_f$ eine Tangente mit der Steigung $m=-2$ angelegt werden kann. [3]

---

Tipp

• Die Gleichung $f^{\prime }(x)=-2$ hat keine reelle Lösung.

3. Ermitteln Sie die exakten Koordinaten des Wendepunkts von $G_f$ . [4]

---

Ergebnis

$W(\frac{7}{3};\frac{125}{108})$ ist der Wendepunkt von $G_f$ .

4. $G_p$ und die Gerade $G_h$ mit der Funktionsgleichung $h(x)=x+2$ schneiden sich im Punkt $A(2;4)$. Zeichnen Sie die Gerade $G_h$ in die obige Abbildung ein und markieren Sie das Flächenstück, das $G_p$, $G_h$ und die $y$-Achse im I. Quadranten des Koordinatensystems einschließen. Berechnen Sie die Maßzahl seines Flächeninhalts. [6]

---

Tipp

Bevor wir integrieren, fassen wir $p(x)-h(x)$ zusammen.

Ergebnis

$A=\frac{7}{2}$

Aufgabe 2

Beim Backen eines Roggenbrotes kann Sauerteig als Triebmittel für den Brotteig verwendet werden. Für den Sauerteig setzt man Mehl und Wasser im selben Verhältnis zueinander an. Milchsäurebakterien in Mehl und Wasser sorgen dafür, dass im Gemisch die notwendige Milchsäure entsteht. Ein frisch angesetzter Sauerteig besitzt zum Zeitpunkt $t_0=0$ einen pH-Wert (Säuregrad) von $6.0$. Nach $40$ Stunden hat der Sauerteig einen pH-Wert von $3.5$.

Das Durchsäuern des Gemisches lässt sich näherungsweise durch die Funktion $p$ mit der Funktionsgleichung $p(t)=3.2+b\cdot e^{-k\cdot t}$ mit $t\ge 0$ und $b,k\in \mathbb{R}$ beschreiben. Dabei steht die Variable $t$ für die Zeit in Stunden ab dem Zeitpunkt $t_0=0$.

Der Funktionswert von p gibt den pH-Wert zum Zeitpunkt $t$ an. Auf das Mitführen von Einheiten während der Rechnungen wird verzichtet. Runden Sie Ihre Ergebnisse sinnvoll.

Aufgabe (a)

Bestimmen Sie die Werte der Parameter b und k. [4]

---

Tipp

Zur Berechnung von $b$ und $k$ benötigen wir zwei Bedingungen.

Ergebnis

$b=2.8$ ; $k=0.056$

Aufgabe (b)

Im Folgenden gilt $p(t)=3.2+2.8\cdot e^{-0.056\cdot t}$ .

1. Der Sauerteig kann ab einem pH-Wert von $4.0$ dem Brotteig zugegeben werden. Bestimmen Sie rechnerisch den Zeitpunkt, ab welchem die Zugabe des Sauerteigs möglich ist. Berechnen Sie die Abnahmegeschwindigkeit des pH-Wertes zu diesem Zeitpunkt. [6]

---

Tipp

• Wir lösen die Gleichung $p(t)=4.0$ .

• Die erste Ableitung von $p$ ist $\dot{p}(t)=-0.1568\cdot e^{-0.056\cdot t}$ .

• Wir setzen die Lösung der Gleichung in $\dot{p}(t)$ ein.

2. Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen der Funktion $p$ im Bereich $0\le t\le 60$ in ein Koordinatensystem. Wählen Sie dazu für beide Achsen einen geeigneten Maßstab.

Aufgabe 3

Ein Hersteller von Tauchflaschen plant ein neues Tauchflaschenmodell. Die Wandstärke des Materials wird vernachlässigt. Die Tauchflasche hat vereinfacht die Form eines geraden Zylinders mit aufgesetzter Halbkugel. Die Firma gibt für die Zylinderhöhe $h$ (in $\mathrm{dm}$) die Bedingung $h(r)=\frac{4}{r}-\frac{3r}{2}$ vor. Bei den Berechnungen wird auf das Mitführen von Einheiten verzichtet. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen.

Aufgabe (a)

Zeigen Sie, dass die Maßzahl des Volumens (in ${\mathrm{dm}}^3$) der Tauchflasche in Abhängigkeit vom Zylinderradius $r$ (in $\mathrm{dm}$) durch die Funktion $V$ mit der Funktionsgleichung $V(r)=-\frac{5}{6}{r}^3\pi +4r\pi$ beschrieben werden kann. [3]

---

Tipp

• Wir geben das Volumen der Tauchflasche allgemein an und ersetzen die Höhe mit der angegebenen Formel.

Aufgabe (b)

Der Hersteller gibt für das neue Modell einen Radius von $0.85\mathrm{dm}$ bis $1.4\mathrm{dm}$ vor. Ermitteln Sie den Radius $r$ , für den das Volumen der Tauchflasche maximal wird und berechnen Sie die Maßzahl dieses maximalen Volumens. [7]

---

Tipp

• Wir berechnen die Koordinaten des absoluten Hochpunktes des Graphen von $V$.

• Die erste Ableitung von $V$ ist $V^{\prime }(r)=-\frac{5}{2}{r}^2\pi +4\pi$ .

Ergebnis

$H(1.26;10.60)$ ist der absolute Hochpunkt.

Stochastik, Teil 2.1

Aufgabe 1

Im Juni und Juli 2024 findet die Fußball-Europameisterschaft in Deutschland statt. Ein Tourismusunternehmen bietet für fußballbegeisterte Kunden diverse Möglichkeiten, an der Veranstaltung in Deutschland teilzunehmen. Im Nachfolgenden werden nur Kunden betrachtet, welche sich für die Fußball-Europameisterschaft interessieren. Fußballbegeisterte Kunden können bei dem Tourismusunternehmen Anreise ($A$), Unterkunft ($U$) und Eintritt zu einem Spiel ($S$) buchen. $50\mathrm{\%}$ aller Fans buchen die Anreise. Von diesen buchen $80\mathrm{\%}$ gleichzeitig eine Unterkunft. Von den Fans, die eigenständig anreisen, buchen $60\mathrm{\%}$ eine Unterkunft. Unabhängig davon, ob die Anreise bzw. die Unterkunft beim Tourismusunternehmen gebucht oder nicht gebucht wurde, bucht ein fester Anteil aller Fans den Eintritt für den Besuch eines Spieles. Von allen Fans entscheiden sich $36\mathrm{\%}$ für das Komplettangebot aus Anreise mit Unterkunft und Eintritt. Das Buchungsverhalten eines beliebig herausgegriffenen fußballbegeisterten Kunden des Tourismusunternehmens wird als Zufallsexperiment aufgefasst.

Aufgabe (a)

Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller acht Elementarereignisse des betrachteten Zufallsexperiments. [5]

---

Tipp

Aus dem Text entnehmen wir $P(\{AUS\})=0.36$ und berechnen $P(S)$ .

Ergebnis

$P(\{A\bar{U}\bar{S}\})=0.01$

Aufgabe (b)

Gegeben sind folgende Ereignisse:

• $E_1:$“Ein zufällig ausgewählter Kunde bucht die Anreise oder den Eintritt zu einem Spiel.“

• $E_2=\{AUS;A\bar{U}\bar{S};\bar{A}\bar{S}U\}$

• $E_3=\overline{\stackrel{―}{E_1}\cup E_2}$

Ermitteln Sie eine aufzählende Mengenschreibweise für $E_3$ . [3]

---

Tipp

Wir verwenden ein Gesetz von De Morgan.

Aufgabe 2

Ein Hotel, welches zur Europameisterschaft ausschließlich mit Fans belegt ist, bietet neben den gewöhnlichen Services zwei zusätzliche Dienste an, welche die Gäste wählen können. Diese sind ein Fahrdienst zum Spiel im örtlichen Stadion ($F$) sowie ein Besuch des Trainingsgeländes der ansässigen Nationalmannschaft ($N$). Von früheren Großereignissen ist bekannt, dass drei von fünf Gästen den Fahrdienst wählen. Insgesamt entscheiden sich $50\mathrm{\%}$ aller Gäste für genau einen der beiden zusätzlichen Dienste. Außerdem gilt: $P_F(N)=0.25$ . Bestimmen Sie mit Hilfe einer Vierfeldertafel, wie viele der insgesamt $400$ Gäste des Hotels keinen der beiden zusätzlichen Dienste wünschen. [5]

Aufgabe 3

Bei der Zusammenstellung der sechs Gruppen für die Gruppenphase wurden zunächst die vermeintlich sechs stärksten Mannschaften zufällig per Los auf die sechs Gruppen verteilt. Diese sechs Mannschaften werden als Gruppenköpfe bezeichnet. Die Wahrscheinlichkeit, dass ein Gruppenkopf unter den 16 Mannschaften, die ins Achtelfinale einziehen, vertreten ist, beträgt p=0.8 . Berechnen Sie die Wahrscheinlichkeit des folgenden Ereignisses $E_4$ . [2]

$E_4=$“Nicht alle Gruppenköpfe erreichen das Achtelfinale.“

---

Ergebnis

$P(E_4)=0.73786$

Aufgabe 4

Ein Fanshop vor einem Stadion bietet den Fans genau die folgenden drei Artikel zum Kauf an.

Artikel	Trikot	Hose	Fahne
Preis in €	$100$	$50$	$10$

Im Folgenden werden nur Fans betrachtet, die mindestens einen der obigen drei Artikel kaufen, wobei kein Fan denselben Artikel mehrfach kauft.

Die Zufallsgröße $X$ beschreibt die Ausgaben in Euro eines Fans im Fanshop. Die folgende Tabelle zeigt die unvollständige Wahrscheinlichkeitsverteilung der Zufallsgröße $X$ .

$x$							$160$
$P(X=x)$	$0.1$	$0.2$	$0.2$	$0.15$	$0.05$	$0.25$	$0.05$

Aufgabe (a)

Vervollständigen Sie die Tabelle, indem Sie die fehlenden Zufallswerte $x$ von links nach rechts der Größe nach aufsteigend in die obere Tabellenzeile eintragen. Berechnen Sie anschließend die durchschnittlichen Tageseinnahmen des Fanshops pro Spieltag, wenn im Fanshop mit durchschnittlich $250$ Fans an einem Spieltag zu rechnen ist. [3]

Aufgabe (b)

Aufgrund der zunehmenden Anzahl an umweltbewussten Fans überlegt der Inhaber des Fanshops nur noch GREEN-Label zertifizierte Trikots und Hosen anzubieten. Er müsste dafür aber die Verkaufspreise dieser Artikel deutlich erhöhen. Ein befreundeter Geschäftsmann behauptet, dass erfahrungsgemäß mindestens $80\mathrm{\%}$ der Fans den Preisanstieg akzeptieren würden und dadurch eine deutliche Gewinnsteigerung zu erwarten sei. Sollte dies der Fall sein, will der Inhaber des Fanshops die Umstellung wagen. Allerdings glaubt er, dass deren Anteil deutlich geringer ist (Gegenhypothese). Um eine Entscheidung zu treffen, befragt er $100$ zufällig ausgewählte Fans, ob diese höhere Preise für die GREEN-Label zertifizierten Produkte in Kauf nehmen würden. Entwickeln Sie für den Inhaber des Fanshops einen geeigneten Hypothesentest auf einem Signifikanzniveau von $5\mathrm{\%}$ . Geben Sie an, welche Entscheidung der Test nahelegt, wenn $75$ Kunden angeben, dass sie die höheren Preise für die GREEN-Label zertifizierten Produkte akzeptieren würden. [5]

---

Ergebnis

$A=\{73,\dots ,100\}$

Stochastik, Teil 2.2

Aufgabe 1

An einer Fachoberschule wird eine Umfrage zu den Zukunftsplänen der Schülerinnen und Schüler durchgeführt. Laut dieser Umfrage möchte nach dem Fachabitur ein Fünftel aller Befragten ein sogenanntes Gap Year ($G$) machen. $70\mathrm{\%}$ davon haben vor, in diesem Jahr ins Ausland zu gehen ($\bar{D}$), alle anderen verbringen die Zeit lieber in Deutschland ($D$). Von denjenigen, die ins Ausland gehen, machen dort $35\mathrm{\%}$ Work & Travel ($W$), $30\mathrm{\%}$ ein Praktikum ($P$) und der Rest andere Tätigkeiten ($T$) wie zum Beispiel Sprachreisen, Urlaub oder arbeiten als Au-pair. Die Hälfte derer, die während ihres Gap Years in Deutschland bleiben, nutzt die Zeit für ein Praktikum und die andere Hälfte für einen Freiwilligendienst ($F$). Von den Befragten, die sich gegen eine Auszeit ($\bar{G}$) nach dem Fachabitur entscheiden, planen $40\mathrm{\%}$ zu studieren ($S$). Der Rest wird zu gleichen Teilen die dreizehnte Klasse ($K$) besuchen oder eine Ausbildung beginnen ($A$). Die Befragung einer zufällig ausgewählten Schülerin oder eines zufällig ausgewählten Schülers nach den Zukunftsplänen wird als Zufallsexperiment aufgefasst.

Aufgabe (a)

Bestimmen Sie unter Verwendung eines Baumdiagramms die Wahrscheinlichkeiten aller acht Elementarereignisse des Zufallsexperiments. [5]

Aufgabe (b)

Gegeben sind die folgenden Ereignisse:

$E_1:$“Eine zufällig ausgewählte befragte Person plant ein Gap Year im Ausland.“

$E_2=\{G\bar{D}P;GDP\}$

$E_3=\overline{E_1\cap E_2}$

Geben Sie $E_1$ in aufzählender Mengenschreibweise an und formulieren Sie $E_2$ möglichst einfach im Sachzusammenhang.

Berechnen Sie anschließend $P(E_3)$ . [4]

---

Tipp

Wir verwenden ein Gesetz von De Morgan.

Ergebnis

$P(E_3)=0.958$

Aufgabe 2

Die Schülerin Lena entscheidet sich für ein Gap Year mit Auslandsaufenthalt in Asien. Sie findet einen Job bei einer Auffangstation für Meerestiere. Im Durchschnitt sind $65$ von $100$ behandelten Tieren Meeresschildkröten ($S$). Insgesamt sind $60\mathrm{\%}$ aller Verletzungen und Krankheiten bei Meerestieren die Folge von Plastikmüll ($M$) in den Ozeanen, zwei Drittel davon treten bei Meeresschildkröten auf. Erstellen Sie für den beschriebenen Sachverhalt eine vollständig ausgefüllte Vierfeldertafel. Bestimmen Sie die Wahrscheinlichkeit des Ereignisses $E_4=M\cup S$ und interpretieren Sie Ihr Ergebnis im Sinne der vorliegenden Thematik. [5]

Aufgabe 3

Eine von Lenas Lieblingsaufgaben in der Auffangstation ist das Freilassen von Baby-Schildkröten an möglichst sicheren Stränden. Sie weiß jedoch, dass die Überlebenschance der Baby-Schildkröten in den ersten paar Tagen aufgrund der hohen Anzahl an Fressfeinden nur bei $10\mathrm{\%}$ liegt. Berechnen Sie die Wahrscheinlichkeit dafür, dass von $20$ freigelassenen Schildkrötenbabys mindestens drei, aber höchstens sieben Tiere überleben. [2]

---

Tipp

Wir rechnen hier mit Bernoulli.

Ergebnis

$P(E_5)=0.32265$

Aufgabe 4

Lena möchte die Reisezeit ihres Work & Travel Aufenthalts nutzen, um Tauchen zu lernen. Eine Tauchschule in Thailand macht Werbung mit der Behauptung, dass bei mindestens $70\mathrm{\%}$ aller Tauchgänge Meeresschildkröten beobachtet werden können. Lena vermutet allerdings, dass der Anteil deutlich geringer ist (Gegenhypothese). Um ihren Verdacht mit einem Hypothesentest zu überprüfen, befragt sie Taucher von 50 verschiedenen Tauchgängen, ob Schildkröten gesehen wurden. Lena möchte sich bei der Annahme ihrer Vermutung mit einer Wahrscheinlichkeit von höchstens $3\mathrm{\%}$ irren.

Aufgabe (a)

Geben Sie für diesen Test die Testgröße sowie die Nullhypothese an. Ermitteln Sie den größtmöglichen Ablehnungsbereich der Nullhypothese und geben Sie an, welche Entscheidung der Test nahelegt, wenn auf genau 20 Tauchgängen keine Meeresschildkröten gesehen werden. [5]

---

Ergebnis

$A=\{29,\dots ,5\text{0}\}$

Aufgabe (b)

Berechnen Sie für den entwickelten Test die Wahrscheinlichkeit des Fehlers 2. Art, wenn tatsächlich nur auf der Hälfte aller Tauchgänge mit der Tauchschule Meeresschildkröten gesehen werden. [2]

---

Ergebnis

$\beta =0.16112$