Prüfung 2024¶
Analysis, Teil 1¶
Aufgabe 1¶
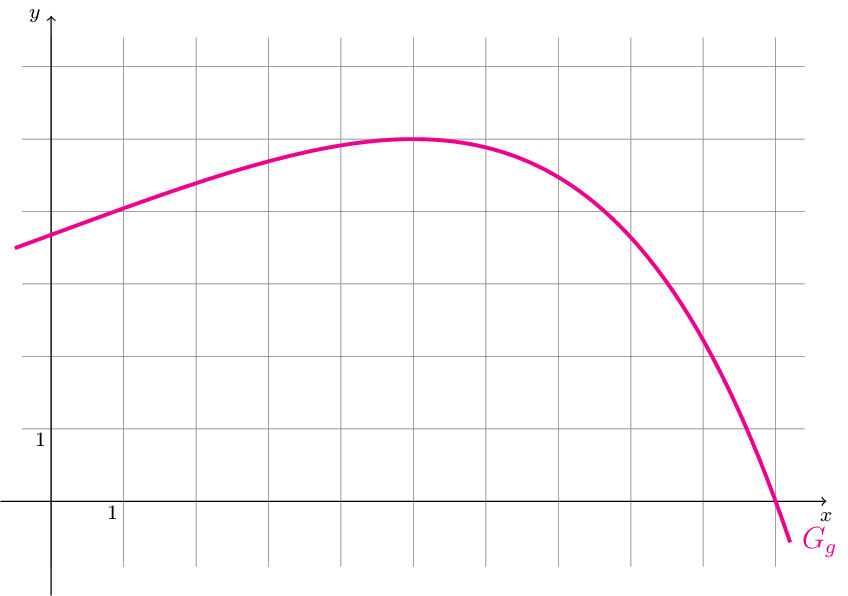
Unten abgebildet ist ein Ausschnitt des Graphen \(G_{g}\) der Funktion \(g\) mit der maximalen Definitionsmenge \(D_{g}=\mathbb{R}\) .
Aufgabe (a)¶
Geben Sie jeweils an, ob die Terme \(g(10)\) und \(g^{\prime\prime}(5)\) Werte haben, die größer, kleiner oder gleich Null sind. [2]
Aufgabe (b)¶
Bestimmen Sie anhand der Abbildung graphisch die Steigung der Tangente an \(G_{g}\) im Punkt \(P(7;g(7))\) . Veranschaulichen Sie Ihr Vorgehen in obiger Abbildung durch ein geeignetes Steigungsdreieck. [3]
Aufgabe (c)¶
Die Funktion \(g\) ist durch die Gleichung \(g(x)=-(x-10)\cdot e^{0.2x-1}\) gegeben. Weisen Sie nach, dass die Funktion mit dem Term \(G(x)=-(5x-75)\cdot e^{0.2x-1}\) mit \(D_{G}=\mathbb{R}\) eine Stammfunktion von \(g\) ist. [3]
Aufgabe (d)¶
Berechnen Sie die genauen Funktionswerte \(G(5)\) und \(G(10)\) . Markieren Sie mit einer Kontur das Flächenstück, dessen Flächenmaßzahl gleich der Differenz \(G(10)-G(5)\) ist und geben Sie die Maßzahl exakt an. [3]
Aufgabe 2¶
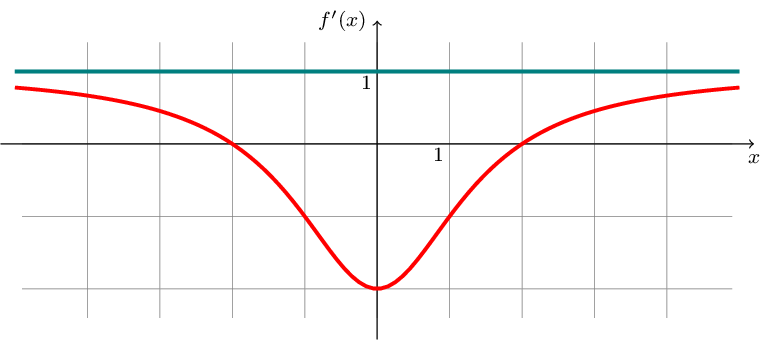
In unteren Diagramm ist ausschnittsweise der Graph \(G_{f^{\prime}}\) der ersten Ableitungsfunktion \(f^{\prime}\) einer Funktion \(f\) mit \(D_{f}=\mathbb{R}\) abgebildet. Der Graph \(G_{f^{\prime}}\) eine waagrechte Asymptote mit der Gleichung \(y=1\) und die Ableitungsfunktion \(f^{\prime}\) hat genau zwei Nullstellen. Der Abbildung dürfen ganzzahlige Werte entnommen werden.
Aufgabe (a)¶
Geben Sie jeweils die Art und die \(x\)-Koordinaten der beiden relativen Extrempunkte von \(G_{f}\) an. [3]
Aufgabe (b)¶
Der Graph \(G_{f}\) hat eine Stelle mit größtem Gefälle. Geben Sie sowohl diese Stelle als auch den Wert des größten Gefälles an. [2]
Aufgabe (c)¶
Der Graph \(G_{f}\) besitzt für \(x\rightarrow\infty\) eine Asymptote. Geben Sie die Art und die Steigung dieser Asymptote an und begründen Sie Ihre Antworten. [2]
Augabe 3¶
Gegeben ist die Funktion \(h\) mit dem Term \(h(x)=\dfrac{1}{x}\cdot\ln(x+1)\) in ihrer maximalen Definitionsmenge \(D_{h}\subseteq\mathbb{R}\) . Ermitteln Sie das Verhalten der Funktionswerte von \(h\) für \(x\rightarrow\infty\) und bei rechtsseitiger Annäherung an die Stelle \(x=-1\) . [4]
Geometrie, Teil 1¶
Aufgabe 1¶
In einem kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) sind die Ebene
\(E:x_{1}+2x_{2}-x_{3}=4\)
und die Geradenschar
\(g_{k}:\vec{x}=\begin{pmatrix}-3\\ 4\\ 1 \end{pmatrix}+r\begin{pmatrix}-2\\ -k-2\\ k \end{pmatrix}\) mit \(r,k\in\mathbb{R}\) gegeben.
Aufgabe (a)¶
Bestimmen Sie die Schnittpunkte der Ebene \(E\) mit den Koordinatenachsen und veranschaulichen Sie die Lage der Ebene \(E\) in dem nachfolgend abgebildeten Koordinatensystem. [4]

Aufgabe (b)¶
Überprüfen Sie, ob ein Wert für \(k\) existiert, so dass die Gerade \(g_{k}\) die Ebene \(E\) senkrecht schneidet. [2]
Aufgabe (c)¶
Die Ebene \(F\) beinhaltet die \(x_{3}\)-Achse und steht senkrecht auf der Ebene \(E\) . Geben Sie eine Gleichung der Ebene \(F\) in Parameterform an. [2]
Aufgabe 2¶
Für die linear unabhängigen Vektoren \(\vec{a}\) , \(\vec{b}\) und \(\vec{c}\) im \(\mathbb{R}^{3}\) gelten zugleich die folgenden drei angegebenen Bedingungen.
\(\vec{a}\cdot\vec{b}=0\)
\(|\vec{a}|=|\vec{b}|=5\)
\(\vec{c}=\frac{1}{5}\cdot(\vec{a}\times\vec{b})\)
Die drei Vektoren \(\vec{a}\) , \(\vec{b}\) und \(\vec{c}\) spannen einen Spat auf. Dabei spannen die Vektoren \(\vec{a}\) und \(\vec{b}\) die Grundfläche des Spats auf. Beschreiben Sie die Form des Spats und legen Sie nachvollziehbar dar, wie Sie zu Ihren Aussagen kommen. [4]
Analysis, Teil 2.1¶
Aufgabe 1¶
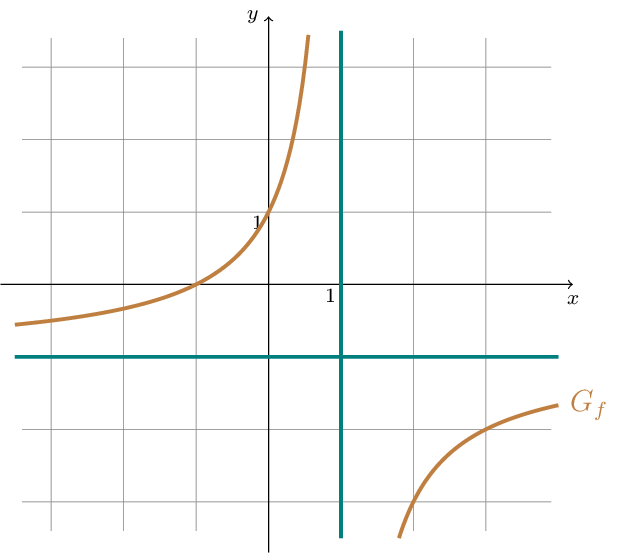
Gegeben ist die Funktion \(f\) durch den Term \(f(x)=\dfrac{x+1}{1-x}\) mit \(x\neq 1\) . Der Graph der Funktion \(f\) heißt \(G_{f}\) . Die Abbildung zeigt einen Teil von \(G_{f}\) mit seinen beiden Asymptoten.
Aufgabe (a)¶
Lesen Sie jeweils die Art und die Gleichung der Asymptoten von \(G_{f}\) ab und geben Sie diese an. [2]
Aufgabe (b)¶
Gegeben ist die Funktion \(g\) mit dem Term \(g(x)=-x\) mit \(D_{g}=\mathbb{R}\) . Der Graph der Funktion \(g\) heißt \(G_{g}\) . Zeichnen Sie \(G_{g}\) in die obige Abbildung ein und berechnen Sie die exakten \(x\)-Koordinaten der Schnittpunkte der Graphen \(G_{f}\) und \(G_{g}\) . [5]
Ergebnis
\(x=1+\sqrt{2}\)
Aufgabe (c)¶
Gegeben sind die bestimmten Integrale \(\int\limits_{1}^{1+\sqrt{2}}(-1-g(x))dx\) und \(\int\limits_{1+\sqrt{2}}^{3}(-1-f(x))dx\) . Die Integralwerte können jeweils geometrisch als Flächenmaßzahl eines Flächenstückes im Koordinatensystem interpretiert werden. Kennzeichnen Sie die beiden Flächenstücke. [3]
Aufgabe (d)¶
Die reelle Funktion \(h\) mit dem Term \(h(x)=\ln\left(f(x)\right)\) besitzt den maximalen Definitionsbereich \(D_{h}=]-1;1[\) . Der Graph der Funktion \(h\) heißt \(G_{h}\) . Der Graph \(G_{h}\) ist punktsymmetrisch zum Ursprung des Koordinatensystems (Nachweis nicht erforderlich!).
Ermitteln Sie mithilfe von \(G_{f}\) das Verhalten der Funktionswerte von \(h\) bei Annäherung an die Ränder von \(D_{h}\) . Geben Sie die Gleichungen aller Asymptoten von \(G_{h}\) an. [4]
Bestätigen Sie rechnerisch, dass \(G_{h}\) keine relativen Extrempunkte besitzt. [6]
Ergebnis
\(h^{\prime}(x)=\dfrac{-2}{x^{2}-1}\)
Zeichnen Sie \(G_{h}\) mit seinen Asymptoten in das vorhandene Koordinatensystem ein. [4]
Aufgabe 2¶
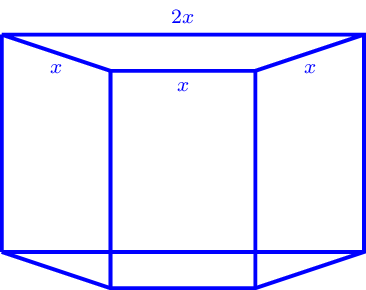
Eine neue Sorte Pralinen soll mit ansprechender Verpackung auf den Markt kommen. Diese hat die abgebildete Form eines geraden Prismas mit trapezförmiger Grundfläche. Das Volumen der Verpackungsschachtel beträgt \(400\,\mathrm{cm^{3}}\) . Die Maßzahl \(A\) der Oberfläche der oben offenen Schachtel in \(\mathrm{cm^{2}}\) lässt sich in Abhängigkeit von der Länge \(x\) in \(\mathrm{cm}\) durch die Gleichung \(A(x)=\frac{3}{4}\sqrt{3}x^{2}+\dfrac{8000\sqrt{3}}{9x}\) mit \(2\leq x\leq 20\) darstellen. Die Maße des Trapezes können aus der Skizze in Abhängigkeit von \(x\) abgelesen werden. Auf die Mitführung der Einheiten kann bei den folgenden Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse falls nicht anders gefordert auf zwei Nachkommastellen.
Aufgabe (a)¶
Im Bild sind zwei mögliche Verpackungsschachteln mit einem Volumen von \(400\,\mathrm{cm^{3}}\) nicht maßstäblich dargestellt. Die eine Schachtel hat die Kantenlänge \(x=11.37\) und die andere Schachtel hat die Kantenlänge \(x=6.00\) . Zeigen Sie, dass beide Schachteln ganzzahlig gerundet den gleichen Oberflächeninhalt haben.
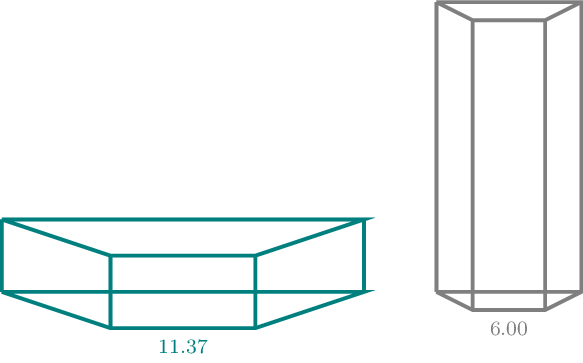
Beide Schachteln verursachen die gleichen Herstellungskosten. Nennen Sie zwei Kriterien, die bei einer Entscheidung für eine der beiden Verpackungsschachteln ausschlaggebend sein können. [4]
Aufgabe (b)¶
Aus Umweltschutzgründen soll die Verpackung eine möglichst geringe Oberfläche \(A\) haben. Ermitteln Sie die Länge \(x\) in \(\mathrm{cm}\) so, dass \(A(x)\) für \(2\leq x\leq 20\) minimal ist und berechnen Sie die Maßzahl des absolut kleinsten Oberflächeninhalts. [6]
Ergebnis
\(A^{\prime}(x)=\frac{3}{2}\sqrt{3}x-\dfrac{8000\sqrt{3}}{9x^{2}}\)
Aufgabe (c)¶
Zeichnen Sie den Graphen \(G_{A}\) der Funktion \(A\) für \(2\leq x\leq 20\) in ein geeignetes Koordinatensystem. Kennzeichnen Sie am Graphen \(G_{A}\) die Punkte \(P_{1}(6;A(6))\) und \(P_{2}(11.37;A(11.37))\) . Geben Sie die Koordinaten des absoluten Hochpunktes von \(G_{A}\) an. [6]
Aufgabe (d)¶
Ein Süßwarenhersteller entscheidet sich für eine Schachtel mit \(x=8\,\mathrm{cm}\) bei einem Volumen von \(400\,\mathrm{cm^{3}}\) . Berechnen Sie die Flächenmaßzahl des trapezförmigen Bodens und die Höhe \(h\) der zugehörigen Schachtel. [3]
Tipp
Die Schachtel ist ein Körper, bei dem die Grundfläche und die Deckfläche gleich sind.
Analysis, Teil 2.2¶
Aufgabe 1¶
Gegeben ist die Funktion \(f\) mit dem Term
\(f(x)=\dfrac{x^{3}-3x+2}{x^{2}}\) und dem Definitionsbereich \(D_{f}=\mathbb{R}\setminus\{0\}\) . Der Graph von \(f\) wird mit \(G_{f}\) bezeichnet.
Aufgabe (a)¶
Zeigen Sie, dass \(f(x)\) zu jedem der beiden folgenden Terme äquivalent ist. [3]
\(f(x)=\dfrac{(x-1)^{2}(x+2)}{x^{2}}\)
\(f(x)=x-\dfrac{3}{x}+\dfrac{2}{x^{2}}\)
Tipp
Wir formen die oberen zwei Terme um und erhalten den Ausgangsterm.
Aufgabe (b)¶
Geben Sie die Nullstellen von \(f\) mit ihrer jeweiligen Vielfachheit an. [2]
Aufgabe (c)¶
Geben Sie zu jeder Asymptote von \(G_{f}\) deren Art und Gleichung an. [2]
Tipp
Wir haben eine senkrechte und eine schräge Asymptote.
Aufgabe (d)¶
Ermitteln Sie die maximalen Monotonieintervalle von \(G_{f}\) und geben Sie die Art seines einzigen lokalen Extrempunktes an. [9]
Ergebnis
\(f^{\prime}(x)=\dfrac{x^{3}+3x-4}{x^{3}}\)
Aufgabe (e)¶
Die Abbildung zeigt ein endliches Flächenstück \(A\) , das unter anderem von \(G_{f}\) begrenzt wird. Berechnen Sie die Maßzahl seines Flächeninhalts. Die ganzzahligen Grenzen des Flächenstücks dürfen der Abbildung entnommen werden. [4]
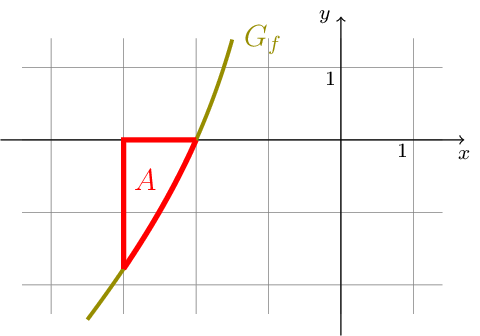
Aufgabe 2¶
Gegeben ist die Funktion \(h\) mit dem Term \(h(x)=2.25\cdot[\ln(x)]^{2}\) mit der Definitionsmenge \(D_{h}=\mathbb{R}^{+}\) . Der Graph von \(h\) wird mit \(G_{h}\) bezeichnet.
Aufgabe (a)¶
Untersuchen Sie das Verhalten der Funktionswerte von \(h\) bei Annäherung an die Ränder von \(D_{h}\) . [3]
Aufgabe (b)¶
Ermitteln Sie die Art und die Koordinaten des relativen Extrempunktes und die exakten Koordinaten des Wendepunktes von \(G_{h}\) . [8]
Ergebnis
\(h^{\prime}(x)=\dfrac{4.5\ln x}{x}\) ; \(h^{\prime\prime}(x)=4.5\dfrac{1-\ln x}{x^{2}}\)
Aufgabe (c)¶
Zeigen Sie mit Hilfe partieller Integration, dass die Funktion \(H\) mit
\(H(x)=2.25\cdot x\cdot[\ln(x)]^{2}-4.5\cdot x\cdot\ln(x)+4.5\cdot x\) mit \(x\in\mathbb{R}^{+}\) eine Stammfunktion von \(h\) ist. [5]
Aufgabe (d)¶
Nun wird zusätzlich die Funktion s mit der Definitionsmenge \(D_{s}=[1;12]\) und dem Term \(s(x)=1.5\cdot\ln x\) betrachtet. Es gilt also \([s(x)]^{2}=h(x)\) für alle \(x\in D_{s}\) . Der Graph von \(s\) wird mit \(G_{s}\) bezeichnet. Lässt man \(G_{s}\) um die \(x\)-Achse rotieren, entsteht ein Rotationskörper (siehe Abbildung), welcher als Modell für den Kelch eines Saftglases dient. Die Koordinaten der Punkte sind Längenangaben in der Einheit Zentimeter. Auf die Mitführung der Einheiten kann bei den folgenden Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen.

Die Volumenmaßzahl \(V\) des obigen Rotationskörpers kann mit dem Integral \(V=\pi\cdot\int\limits_{1}^{12}[s(x)]^{2}dx\) berechnet werden. Zeigen Sie rechnerisch, dass das Saftglas ein maximales Flüssigkeitsvolumen von ca. \(257\,\mathrm{ml}\) aufnehmen kann. [4]
Die Standfläche des Saftglases soll kreisförmig sein und den gleichen Durchmesser wie die Querschnittsfläche des Rotationskörpers für \(x=12\) haben. Ermitteln Sie die Maßzahl des Flächeninhalts dieser Standfläche. [3]

Tipp
Hier berechnen wir einfach \(s(12)\) und erhalten den Radius des Sockels.
Geometrie, Teil 2.1¶
Aufgabe 1¶
Für die Bühnenbeleuchtung einer Theateraufführung an einer Schule wird ein Scheinwerfer installiert. Die Position des Scheinwerfers und der von ihm ausgeleuchtete Raum auf der Bühne wird modellhaft in einem kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) beschrieben. Die \(x_{1}x_{2}\)-Ebene des Koordinatensystems wird durch den Bühnenboden festgelegt. Die rechteckige Glasfläche des Scheinwerfers hat die Ecken \(A(2;0;31)\) , \(B(-1;2;30)\) , \(C(-2;0;29)\) und \(D(1;-2;30)\) .
Die Vollausleuchtung mit dem Scheinwerfer ohne Berücksichtigung des Halbschattens kann in guter Näherung durch den Körper \(PQRTABCD\) beschrieben werden. Die Punkte \(P(\frac{130}{3};\frac{31}{3};0)\) , \(Q(6.5;24.5;0)\) , \(R(-2;5.8;0)\) und \(T(23.5;-9.5;0)\) sind die Eckpunkte der ausgeleuchteten Fläche \(PQRT\) auf dem Bühnenboden. Die Koordinaten sind Längenangaben in der Einheit Dezimeter (\(\mathrm{dm}\)). Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden. Die Ergebnisse sind sinnvoll zu runden.

Aufgabe (a)¶
Die Gerade \(g_{QB}\) verläuft durch die Punkte \(Q\) und \(B\) . Die Gerade \(g_{RC}\) verläuft durch die Punkte \(R\) und \(C\) . Die Geraden \(g_{QB}\) und \(g_{RC}\) schneiden sich im Punkt \(S\) . Berechnen Sie die Koordinaten des Punktes \(S\). [6]
Ergebnis
\(S(-2;-1;34)\)
Aufgabe (b)¶
Stellen Sie eine Gleichung der Lotgeraden zur Ebene \(E\) , in der sich die Glasfläche \(ABCD\) befindet, durch den Punkt \(S\) auf und bestimmen Sie den Abstand des Punktes \(S\) zur Ebene \(E\) . [8]
Ergebnis
Eine Gleichung der Lotgeraden ist \(l:\vec{x}=\begin{pmatrix}0\\ 0\\ 30 \end{pmatrix}+\rho\begin{pmatrix}-2\\ -1\\ 4 \end{pmatrix}\) .
Der gesuchte Abstand \(d\) ist \(\sqrt{21}\approx 4.58\) .
Aufgabe (c)¶
Die Diagonalen des Vierecks \(PQRT\) schneiden sich im Punkt \(M(15;7.5;0)\) (Nachweis nicht erforderlich). Zeigen Sie, dass der Punkt \(M\) auf der Geraden \(l\) liegt. Berechnen Sie die Größe des Schnittwinkels der Geraden \(l\) mit der \(x_{1}x_{2}\)-Koordinatenebene. [4]
Ergebnis
\(\varphi\approx60.79^{\circ}\)
Aufgabe (d)¶
Der Scheinwerfer besitzt einen Flügelbegrenzer. Der einzustellende Winkel soll für den rechten Flügel berechnet werden. Vereinfachend soll angenommen werden, dass der rechte Flügel in der Ebene \(F\) liegt, die durch die Punkte \(B\) , \(A\) und \(Q\) festgelegt ist. Berechnen Sie die Größe des Schnittwinkels zwischen der Ebene \(E\) und der Ebene \(F\) .
Schließen Sie anschließend auf die Größe des einzustellenden Winkels \(\beta\) zwischen der Glasfläche des Scheinwerfers und dem rechten Flügel des Flügelbegrenzers. [5]

Tipp
Laut Skizze ist der gesuchte Winkel \(\beta\) ein stumpfer Winkel.
Ergebnis
\(\beta\approx 104.96^{\circ}\)
Geometrie, Teil 2.2¶
Aufgabe 1¶
Für einen Stand auf der nächsten Reisemesse in Müchnen plant ein Veranstalter ein Zelt, das in einem kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) modellhaft durch eine Pyramide \(OABCS\) mit quadratischer Grundfläche dargestellt wird. Die Zeltwand \(OAS\) liegt in der Ebene \(H:-93x_{2}+50x_{3}=0\) . Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter. Auf die Mitführung von Einheiten kann bei den Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.

Aufgabe (a)¶
Auch nach der Corona-Pandemie wird in den Zelten auf der Reisemesse auf eine Beschränkung der Anzahl der sich gleichzeitig im Zelt aufhaltenden Personen geachtet. Die Kenndaten der eingebauten Lüftungsanlage geben für das hier betrachtete Zelt eine Obergrenze von \(0.2\) Personen pro Kubikmeter Raumvolumen vor. Ermitteln Sie, wie viele Personen sich gleichzeitig im betrachteten Zelt aufhalten dürfen. [3]
Tipp
Wir berechnen die Volumenzahl der Pyramide.
Ergebnis
\(62\) Personen
Aufgabe (b)¶
Die Zeltwände dienen als Projektionsflächen für Beamer, die außerhalb des Zeltes montiert sind. Auf die Zeltwand, an der sich der Zelteingang befindet, wird nicht projiziert.
Damit die Projektionen gut sichtbar sind, werden die drei Zeltwände vollständig mit einer speziellen Folie beklebt. Ein Quadratmeter dieser Folie kostet \(15.30\) €. Ermitteln Sie die hierfür anfallenden Materialkosten. [4]
Tipp
Die drei Zeltwände haben die gleiche Fläche, weil die Grundfläche der Pyramide ein Quadrat ist.
Ergebnis
Preis: \(2423.52\) €
Das Objektiv des Beamers, welcher auf die Zeltwand \(OAS\) projiziert, befindet sich im Punkt \(P(5;0;4)\) . Laut Herstellerangabe soll zwischen dem Objektiv des Beamers und der Projektionsfläche ein Mindestabstand von \(1.8\) Meter eingehalten werden. Überprüfen Sie rechnerisch, ob diese Vorgabe hier erfüllt ist. [5]
Tipp
Wir berechnen den Abstand von \(P\) zu der Ebene \(H\) , die das Dreieck \(OAS\) enthält.
Aufgabe (c)¶
Jeweils zwei benachbarte Zeltwände schließen im Inneren des Zeltes einen stumpfen Winkel ein. Ermitteln Sie die Größe dieses Winkels. [5]
Tipp
Wir berechnen den Normalenvektor der Ebene, die das Dreieck \(OCS\) enthält.
Aufgabe (d)¶
Der Zelteingang \(DEFG\) hat eine Durchgangshöhe von \(2.79\,\mathrm{m}\) . Der Punkt \(G\) liegt auf der Strecke \(\overline{DS}\) und der Punkt \(F(8.5;6.05;2.79)\) liegt auf der Strecke \(\overline{ES}\) . Ermitteln Sie die Koordinaten des Punktes \(G\) und zeigen Sie mit Ihrem Ergebnis, dass das Viereck \(DEFG\) ein gleichschenkliges Trapez ist. [6]
Ergebnis
\(G(8.5;3.95;2.79)\)