Prüfung 2023¶
Analysis, Teil 1¶
Aufgabe 1¶
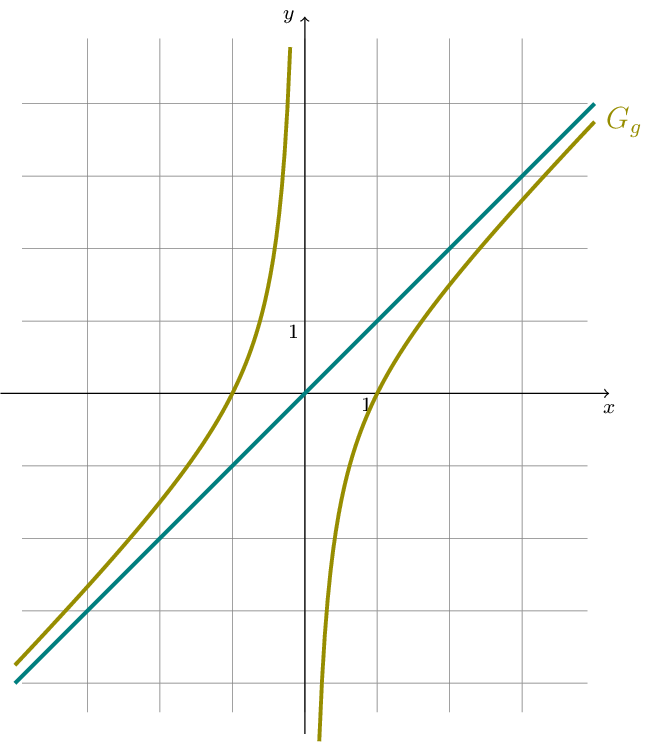
Die Abbildung zeigt den Graphen \(G_{g}\) einer gebrochen-rationalen Funktion \(g\) mit der Definitionsmenge \(D_{g}=\mathbb{R}\setminus\{0\}\) . Der Graph \(G_{g}\) ist punktsymmetrisch zum Koordinatenursprung, besitzt keine lokalen Extrempunkte und hat genau eine schiefe und genau eine senkrechte Asymptote.
Aufgabe (a)¶
Lesen Sie die Nullstellen der Funktion \(g\) und die Gleichungen der Asymptoten des Graphen \(G_{g}\) ab und geben Sie diese an. [2]
Tipp
Laut Angabe müssen wir die Art der Asymptoten eigentlich nicht angeben.
Aufgabe (b)¶
Wir betrachten den Term \(\left|\int\limits_{-3}^{-2}g(x)dx\right|\) . Der Wert diese Terms kann geometrisch als Inhalt einer Fläche im obigen Koordinatensystem von interpretiert werden. Kennzeichnen Sie mit einer Kontur dieses zugehörige Flächenstück im Koordinatensystem oben. [2]
Aufgabe (c)¶
Begründen Sie, dass der Graph \(G_{g^{\prime}}\) der Ableitungsfunktion \(g^{\prime}\) die waagrechte Asymptote mit der Gleichung \(y=1\) besitzt. Zeichnen Sie sämtliche Asymptoten von \(G_{g^{\prime}}\) in das obige Koordinatensystem ein und skizzieren Sie \(G_{g^{\prime}}\) in dieses Koordinatensystem. [5]
Aufgabe (d)¶
\(G\) ist eine Stammfunktion von \(g\) mit \(D_{G}=\mathbb{R}\setminus\{0\}\) . Der Graph der Stammfunktion \(G\) wird mit \(G_{G}\) bezeichnet. Geben Sie für jede der folgenden Aussagen jeweils an, ob Sie wahr oder falsch ist. [4]
\(G_{G}\) besitzt ein relatives Maximum an der Stelle \(x=-1\) .
\(G_{G}\) ist streng monoton steigend im Intervall \(]-\infty;0[\) .
\(G_{G}\) ist linksgekrümmt im Intervall \(]0;+\infty[\) .
\(G(3)-G(1)<5\)
Aufgabe 2¶
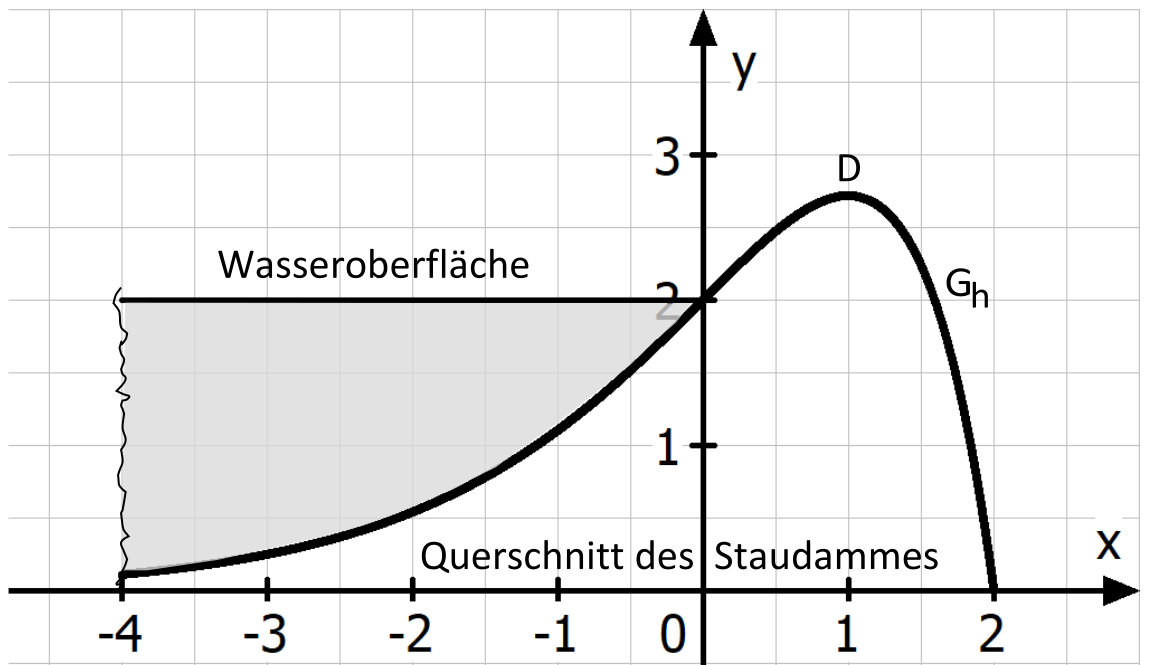
Die Abbildung zeigt modellhaft den Querschnitt eines Staudammes, der \(100\) Meter lang ist. Die Querschnittsfläche des Staudamms hat über die gesamte Länge hinweg die gleiche Form. Die krummlinige Begrenzungslinie der Querschnittsfläche kann durch den Graphen der Funktion \(h\) mit \(h(x)=(2-x)e^{x}\) und \(D_{h}=[-4;2]\) in einem kartesischen Koordinatensystem dargestellt werden. Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität. Bei den Rechnungen kann auf die Mitführung der Einheiten verzichtet werden.
Aufgabe (a)¶
Der Punkt \(D\) ist der höchste Punkt des Staudammes. Berechnen Sie die Koordinaten des Punktes \(D\) . Weisen Sie auch nach, dass ein relativer Hochpunkt vorliegt. [5]
Aufgabe (b)¶
Ein Kubikmeter des zur Aufschüttung des Staudamms verwendeten Materials hat die Masse \(1.8\) Tonnen. Aufgrund der Verdichtung des Materials beim Bau des Staudamms ist das Volumen des tatsächlich benötigten Materials um \(6~\%\) höher, als das theoretisch berechnete. Stellen Sie einen Ansatz auf, mit dem man die Masse des aufgeschütteten Materials in Tonnen berechnen kann. Hier soll die Berechnung nicht durchgeführt werden. [4]
Geometrie, Teil 1¶
Aufgabe 1¶
In einem kartesischen Koordinatensystem des \(\mathbb{R}^{2}\) ist je ein Repräsentant der Vektoren \(\vec{a}\) und \(\vec{b}\) gegeben.
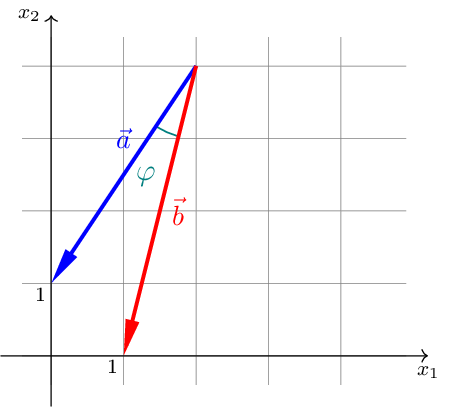
Der Winkel zwischen den beiden Vektoren \(\vec{a}\) und \(\vec{b}\) kann mit der Gleichung \(\cos(\alpha)=\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\) berechnet werden. In einer der drei nachfolgenden Gleichungen ist der Term \(\dfrac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\) richtig berechnet. Entscheiden Sie begründet, welche der untenstehenden Gleichungen die richtige ist. [3]
\(\cos(\alpha)=\frac{12}{\sqrt{13}\cdot\sqrt{18}}\)
\(\cos(\alpha)=\frac{14}{\sqrt{13}\cdot\sqrt{17}}\)
\(\cos(\alpha)=\frac{14}{\sqrt{3}\cdot\sqrt{5}}\)
Aufgabe (b)¶
Zeichnen Sie einen Repräsentanten des Vektors \(\vec{c}=\vec{b}-\vec{a}\) in das Koordinatensystem von oben ein. [1]
Aufgabe (c)¶
Zeigen Sie rechnerisch, dass die Vektoren \(\vec{a}\) und \(\vec{b}\) linear unabhängig sind. [2]
Aufgabe 2¶
In einem kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) sind die drei Punkte \(A(2;0;0)\) , \(B(5;0;0)\) und \(C(4;1;-1)\) gegeben.
Aufgabe (a)¶
Zeigen Sie, dass der Winkel an der Ecke \(C\) im Dreieck \(ABC\) ein rechter Winkel ist. [3]
Aufgabe (b)¶
Berechnen Sie die Maßzahl des Flächeninhalts des Dreiecks \(ABC\) . [3]
Analysis, Teil 2.1¶
Aufgabe 1¶
Gegeben ist die Funktion \(f\) mit dem Term \(f(x)=\dfrac{1}{x+1}+\ln(x+1)\) mit ihrer maximale Definitionsmenge \(D_{f}\subset\mathbb{R}\) . Der Graph von \(f\) wird mit \(G_{f}\) bezeichnet.
Aufgabe (a)¶
Zeigen Sie, dass die Funktion \(f\) die maximale Definitionsmenge \(D_{f}=]-1;+\infty[\) besitzt. [3]
Aufgabe (b)¶
Ermitteln Sie die größtmöglichen Monotonieintervalle der Funktion \(f\) und die Art sowie die Koordinaten des einzigen Extrempunktes von \(G_{f}\) . [7]
Ergebnis
\(f^{\prime}(x)=\dfrac{x}{(x+1)^{2}}\)
Aufgabe (c)¶
Ermitteln Sie die Koordinaten des Wendpunktes von \(G_{f}\) . [5]
Ergebnis
\(f^{\prime\prime}(x)=\dfrac{-x+1}{(x+1)^{3}}\)
Aufgabe (d)¶
Der Graph \(G_{f}\) besitzt die senkrechte Asymptote \(x=-1\) . Zeichnen Sie \(G_{f}\) im Bereich \(-1\leq x\leq6\) unter Verwendung vorliegender Ergebnisse und weiterer geeigneter Funktionswerte sowie die senkrechte Asymptote in ein kartesisches Koordinatensystem. Geben Sie auch die Wertemenge der Funktion \(f\) an. [5]
Tipp
Wir berechnen zusätzlich einige Funktionswerte.
Aufgabe (e)¶
Die Funktion \(F(x)=(x+2)\ln(x+1)-x\) ist in ihrer Definitionsmenge \(D_{F}=D_{f}\) eine Stammfunktion von \(f\) (Nachweis nicht nötig!).
Zeigen Sie, dass gilt: \(\int\limits_{0}^{5}f(x)dx\approx7.54\) . [2]
Aufgabe (f)¶
Markieren Sie in der erstellten Zeichnung mit einer Kontur die beiden Flächenstücke, deren Flächenmaßzahlen \(A_{1}\) und \(A_{2}\) durch folgende Integrale berechnet werden können.
\(A_{1}=\int\limits_{0}^{5}(f(x)-1)dx\) ; \(A_{2}=\int\limits_{0}^{5}(2-f(x)dx\) .
Ermitteln Sie \(A_{1}\) auf zwei Nachkommastellen gerundet. [4]
Aufgabe 2¶
Die folgende Tabelle gibt die Entwicklung der Anzahl der verkauften Bücher eines Bandes wieder. Immer am Ende einer vollen Woche werden die Verkaufszahlen beim Verlag dokumentiert. Dabei bezeichnet \(t\) die Anzahl der Wochen ab Verkaufsstart (\(t=0\)) und \(n(t)\) die Anzahl der verkauften Bücher pro Woche in Tausend. Aufgrund eines einwöchigen Vorbestellungszeitraums werden beim Verkaufsstart bereits \(26800\) Bücher und nach einer Woche weitere \(30000\) verkauft.
\(\small t\) |
\(\small 0\) |
\(\small 1\) |
\(\small 2\) |
\(\small 3\) |
\(\small 4\) |
\(\small 5\) |
\(\small 8\) |
\(\small 10\) |
\(\small n(t)\) |
\(\small 26.8\) |
\(\small 30.0\) |
\(\small 32.3\) |
\(\small 35.0\) |
\(\small 37.5\) |
\(\small 39.5\) |
\(\small 37.6\) |
\(\small 33.2\) |
Aufgabe (a)¶
Stellen Sie die Zuordnung \(n(t)\) in einem geeigneten Koordinatensystem grafisch dar. Verbinden Sie die Punkte zu einer glatten Kurve und formulieren Sie eine Hypothese, wie sich die Verkaufszahlen nach der 10. Woche verhalten werden. [4]
Aufgabe (b)¶
Ausgehend von den Tabellenwerten wird für die Anzahl \(v(t)\) der wöchentlich verkauften Bücher in Tausend ein mathematisches Modell mit dem Term \(v(t)=\dfrac{3000}{t^{2}-12t+111}\) mit \(t\geq0\) entwickelt. Mit der Funktion \(v\) sollen Prognosen angestellt werden, die über die 10. Woche hinausgehen.
Das Modell wird als aussagekräftig und realitätsnah eingestuft, wenn die tatsächlichen Werte von den berechneten um weniger als \(5~\%\) abweichen. Zur Überprüfung werden in der folgenden Tabelle die beiden Hilfsfunktionen \(u\) und \(o\) herangezogen mit \(u(t)=0.95\cdot v(t)\) und \(o(t)=1.05\cdot v(t)\) .
\(\small t\) |
\(\small 0\) |
\(\small 1\) |
\(\small 2\) |
\(\small 3\) |
\(\small 4\) |
\(\small 5\) |
\(\small 8\) |
\(\small 10\) |
\(\small u(t)\) |
\(\small 25.7\) |
\(\small 28.5\) |
\(\small 31.3\) |
\(\small 33.9\) |
\(\small 36.1\) |
\(\small 37.5\) |
\(\small 36.1\) |
\(\small 31.3\) |
\(\small n(t)\) |
\(\small 26.8\) |
\(\small 30.0\) |
\(\small 32.3\) |
\(\small 35.0\) |
\(\small 37.5\) |
\(\small 39.5\) |
\(\small 37.6\) |
\(\small 33.2\) |
Berechnen Sie die Werte für \(o(t)\) und beurteilen Sie, ob die Funktion \(v\) als realitätsnah bezeichnet werden kann. [3]
Tipp
Wir berechnen die Werte von o aus den Werten von u und verwenden dazu den Faktor \(\frac{21}{19}\) .
Ermitteln Sie, in der wievielten Woche nach dem Modell die Verkaufszahl \(4000\) Bücher pro Woche beträgt. [4]
Berechnen Sie die Art und die Koordinaten des relativen Extrempunktes des Graphen der Funktion \(v\) und interpretieren Sie Ihre Ergebnisse im Sachzusammenhang. [6]
Ergebnis
\(\dot{v}(t)=-\dfrac{6000(t-6)}{(t^{2}-12t+111)^{2}}\)
Analysis, Teil 2.2¶
Aufgabe 1¶
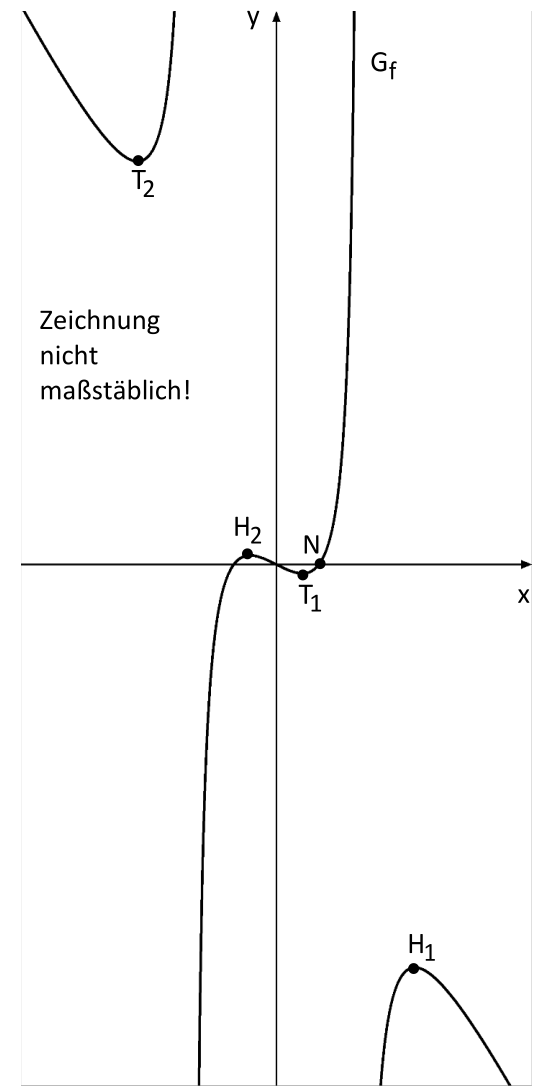
Betrachtet wird die Funktion \(f\) mit dem Term \(f(x)=\dfrac{x^{3}-x}{4-x^{2}}\) und ihrer maximalen Definitionsmenge \(D_{f}\subset\mathbb{R}\) . Die Abbildung zeigt einen Ausschnitt des Graphen \(G_{f}\) der Funktion \(f\) .
Aufgabe (a)¶
Bestimmen Sie \(D_{f}\) sowie die Nullstellen von \(f\) und geben Sie jeweils die Art der Definitionslücken von \(f\) an. [4]
Aufgabe (b)¶
\(G_{f}\) besitzt genau vier lokale Extrempunkte. Die Koordinaten der beiden Extrempunkte \(H_{1}\) und \(T_{1}\) ergeben sich auf zwei Nachkommastellen gerundet zu \(H_{1}(3.26;-4.74)\) und \(T_{1}(0.61;-0.11)\) . Zeigen Sie rechnerisch, dass \(G_{f}\) punktsymmetrisch zum Ursprung ist und geben Sie anschließend die gerundeten Koordinaten der Extrempunkte \(H_{2}\) und \(T_{2}\) an. [4]
Tipp
Bei Symmetrieuntersuchungen formen wir den Term \(f(-x)\) um.
Aufgabe (c)¶
Ermitteln Sie für jede Asymptote von \(G_{f}\) ihre Art und ihre Gleichung. [4]
Aufgabe (d)¶
\(G_{f}\) schneidet die \(x\)-Achse für \(x>0\) im Punkt \(N\) (siehe Abbildung). Ermitteln Sie die Gleichung der Tangente an \(G_{f}\) im Punkt \(N\) . [5]
Ergebnis
\(f^{\prime}(x)=\dfrac{-x^{4}+11x^{2}-4}{(4-x^{2})^{2}}\)
Aufgabe (e)¶
Gegeben sind die Gleichungen der zweiten, dritten und vierten Ableitungsfunktion der Funktion \(f\) .
\(f^{\prime\prime}(x)=\dfrac{6(x^{3}+12x)}{(4-x^{2})^{3}}\)
\(f^{\prime\prime\prime}(x)=\dfrac{18(x^{4}+24x^{2}+16)}{(4-x^{2})^{4}}\)
\(f^{(4)}(x)=\dfrac{72(x^{5}+40x^{3}+80x)}{(4-x^{2})^{5}}\)
Außerdem betrachten wir die fünfte Ableitung \(f^{(5)}(x)=\dfrac{a(x^{b}+60x^{c}+240x^{d}+64)}{(4-x^{2})^{6}}\) .
Untersuchen Sie die vierte Ableitungsfunktion \(f^{(4)}\) auf Nullstellen. Ermitteln Sie ausgehend von den gegebenen Ableitungen die Werte für \(a\) , \(b\) , \(c\) und \(d\) im Term der fünften Ableitungsfunktion \(f^{(5)}\) . [5]
Aufgabe 2¶
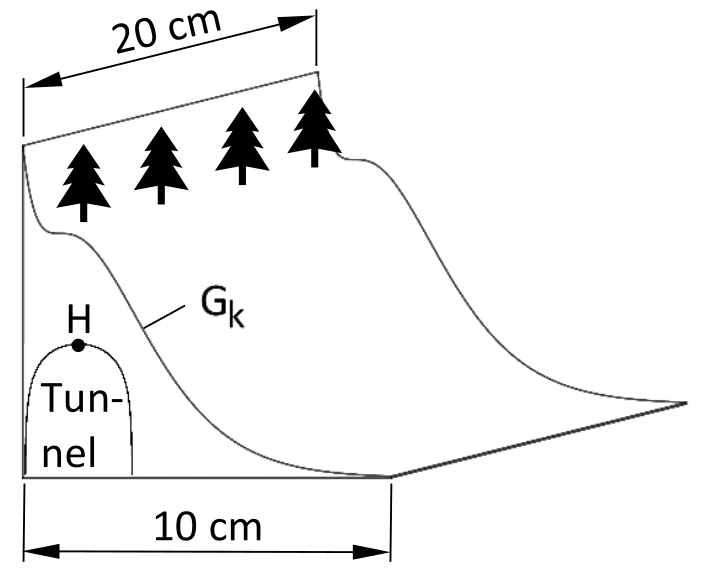
Für den Hintergrund einer Modelleisenbahn soll mithilfe eines 3D-Druckers eine Berglandschaft gedruckt werden. Der Graph \(G_{k}\) der Funktion \(k\) mit dem Term \(k(x)=a(x^{2}+1)\cdot e^{-x}\) mit \(a\in\mathbb{R}\) und dem Definitionsbereich \(D_{k}=[0;10]\) beschreibt die obere Kontur der Berglandschaft. Die Variable \(x\) gibt den Abstand vom linken Rand der Berglandschaft in \(\mathrm{cm}\) und der Funktionswert \(k(x)\) die Höhe der Konturlinie in \(\mathrm{cm}\) über dem Boden an. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.
Aufgabe (a)¶
Die Funktion \(k\) ist im gesamten Definitionsbereich streng monoton abnehmend. Bestimmen Sie den Wert des Parameters \(a\), wenn die Berglandschaft an ihrem höchsten Punkt \(9\mathrm{\,cm}\) hoch sein soll. [2]
Ergebnis
\(a=9\)
Aufgabe (b)¶
Nun rechnen wir mit \(k(x)=9(x^{2}+1)\cdot e^{-x}\) weiter. An der Berglandschaft sollen Bäumchen befestigt werden. Damit diese aufrecht stehen, müssen sie an einer Stelle mit waagrechter Tangente angebracht werden. Berechnen Sie dazu die Koordinaten des Punktes auf der Konturlinie, der diese Bedingung erfüllt. [5]
Aufgabe (c)¶
Zeigen Sie, dass die Funktion \(K\) mit dem Term \(K(x)=-9(x^{2}+2x+3)\cdot e^{-x}\) und \(D_{k}=[0;10]\) eine Stammfunktion von \(k\) ist. Bestimmen Sie den Wert des Integrals \(I=20\cdot\int_{0}^{10}k(x)dx\) und interpretieren Sie Ihr Ergebnis im Sachzusammenhang. [5]
Ergebnis
\(I\approx539\)
Aufgabe (d)¶
Zur Herstellung der Berglandschaft wird Kunstharz zu einem Preis von \(59.90\) € für \(1000\,\mathrm{cm^{3}}\) benötigt. Ermitteln Sie den Materialpreis für eine Berglandschaft gleicher Form, die nicht \(20\,\mathrm{cm}\) sondern ein Meter lang ist. Verluste an Kunstharz durch den Herstellungsprozess sollen dabei nicht berücksichtigt werden. [2]
Tipp
Wir verwenden hier den Faktor \(5\) .
Aufgabe (e)¶
Nun wird zusätzlich die Funktion \(h\) mit dem Term \(h(x)=\ln(-x^{2}+4x)+2\) in dem maximalen Definitionsbereich \(D_{h}=]0;4[\) betrachtet. Der Teil des Graphen \(G_{h}\) der Funktion \(h\) , der über der \(x\)-Achse liegt, beschreibt die Begrenzungslinie eines Tunnels (siehe Bild), der nach der Herstellung durch den 3D-Drucker in die Berglandschaft gefräst werden soll.
Für die Kalibrierung der Fräse werden die Schnittpunkte von \(G_{h}\) mit der \(x\)-Achse benötigt. Ermitteln Sie die \(x\)-Koordinaten dieser Schnittpunkte. [3]
Der Punkt \(H\) (siehe Bild) ist der höchste Punkt des Tunnels (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten des Punktes \(H\) . [4]
Geometrie, Teil 2.1¶
Aufgabe 1¶
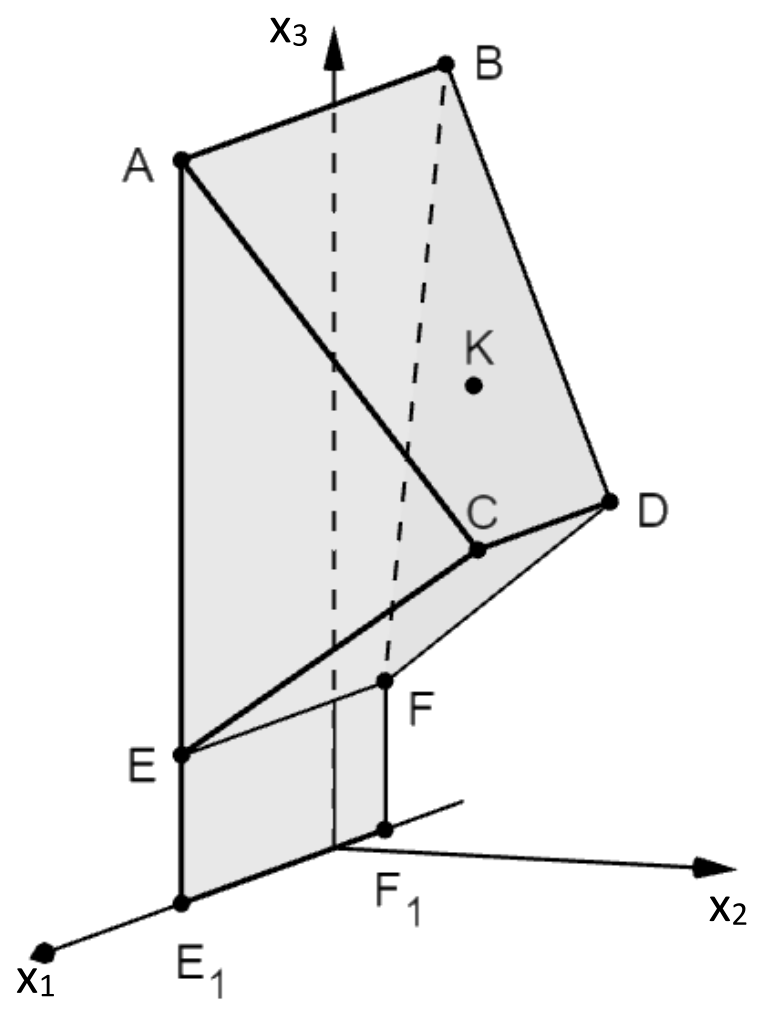
In einer Kletterhalle für Kinder soll eine Wand mit Überhang gebaut werden, welche modellhaft in einem geeignet gewählten kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) betrachtet wird. Der Boden der Kletterhalle liegt in der \(x_{1}x_{2}\)-Ebene. Die Ebene \(G\) , die den Überhang bildet, ist durch die Punkte \(E(15;0;5)\) , \(C(12;9;12)\) und \(D(-1;9;12)\) festgelegt. Zudem sind die Punkte \(A(15;0;25)\) , \(B(-11;0;25)\) und \(F(2;0;5)\) gegeben. Die Koordinaten der Punkte sind Längenangaben in der Einheit Dezimeter. Auf die Mitführung von Einheiten während der Rechnung kann verzichtet werden. Ergebnisse sind gegebenenfalls auf eine Nachkommastelle zu runden.
Aufgabe (a)¶
Bestimmen Sie eine Gleichung der Ebene \(G\) in Koordinatenform und beschreiben Sie die besondere Lage von \(G\) im Koordinatensystem. [5]
Ergebnis
\(G:7x_{2}-9x_{3}+45=0\)
Aufgabe (b)¶
Berechnen Sie den Neigungswinkel der Ebene \(G\) zum Boden. [3]
Ergebnis
\(\alpha\approx37.9^{\circ}\)
Aufgabe (c)¶
Berechnen Sie die Flächenzahl des dreieckigen Seitenteils \(AEC\) . [3]
Ergebnis
\(A=30\sqrt{10}\)
Aufgabe (d)¶
Die Decke der Halle, an der eine Überwachungskamera angebracht werden soll, liegt in der Ebene \(H:x_{3}-26=0\) . Um alle Bereiche der Kletterwand zu erfassen, muss die Kamera weit genug von der Rückwand \(AE_{1}F_{1}B\) entfernt sein. Bestimmen Sie eine Gleichung der Schnittgeraden \(s\) der Ebene G und der Ebene \(H\) . Der Abstand dieser Schnittgeraden \(s\) zur \(x_{1}x_{3}\)-Ebene entspricht dem Mindestabstand der Kamera von der Rückwand \(AE_{1}F_{1}B\) in Dezimeter. Ermitteln Sie diesen Abstand. [4]
Ergebnis
\(d(s;x_{1}x_{2}\text{-Ebene})=27\)
Aufgabe (e)¶
Der Punkt \(K\) ist der Schnittpunkt der beiden Diagonalen des Vierecks \(ACDB\) . Zur Stabilisierung wird innerhalb der Kletterwand ein Stahlträger am Punkt \(K\) angebracht, der senkrecht zur Kletterfläche \(ACDB\) steht. Beschreiben Sie, wie der Montagepunkt des Stahlträgers an der Rückwand \(AE_{1}F_{1}B\) ermittelt werden kann, ohne die Rechnung durchzuführen. [4]
Aufgabe (f)¶
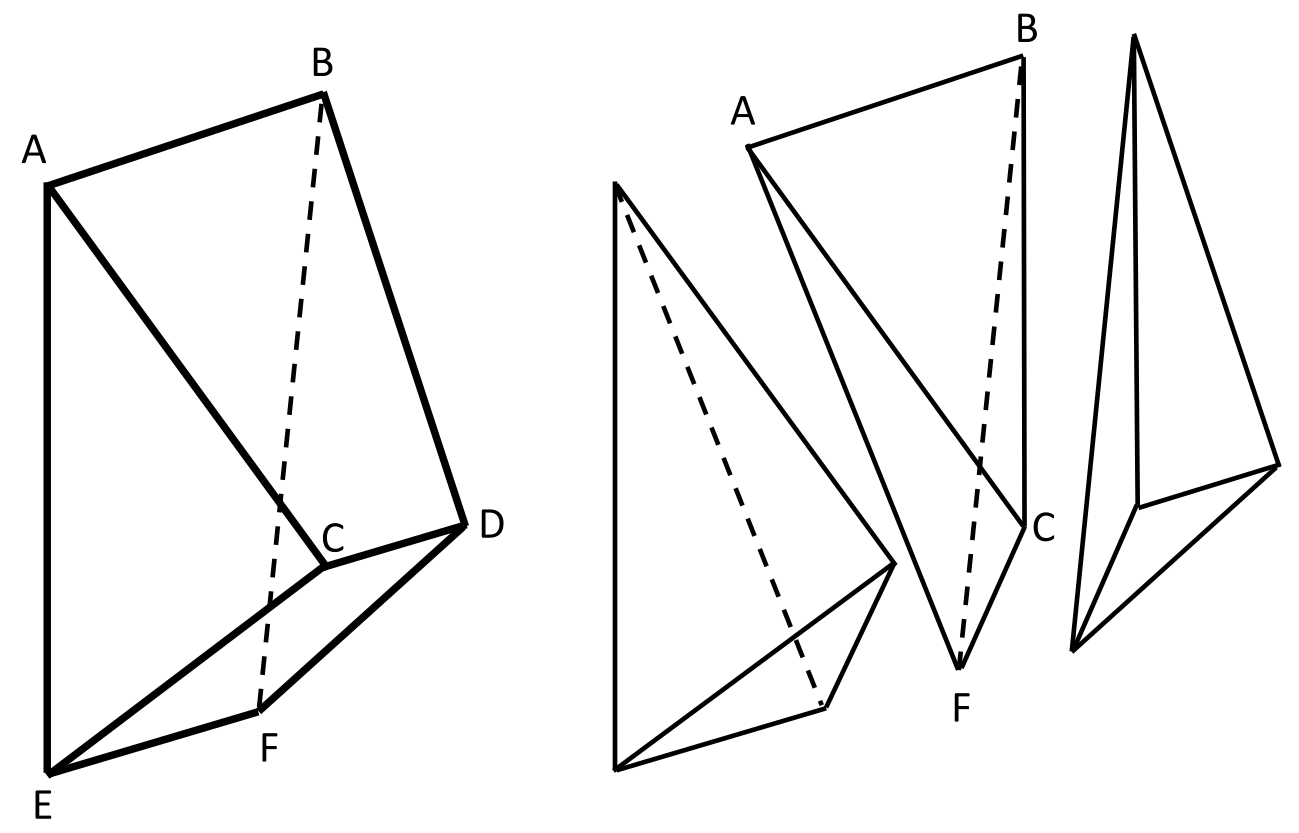
Der Körper \(ABCDEF\) kann in drei Teilkörper zerlegt werden (siehe Skizze). Berechnen Sie die Maßzahl des Volumens der dreiseitigen Pyramide \(ABCF\) . [4]
Ergebnis
\(V=780\)
Geometrie, Teil 2.2¶
Aufgabe 1¶
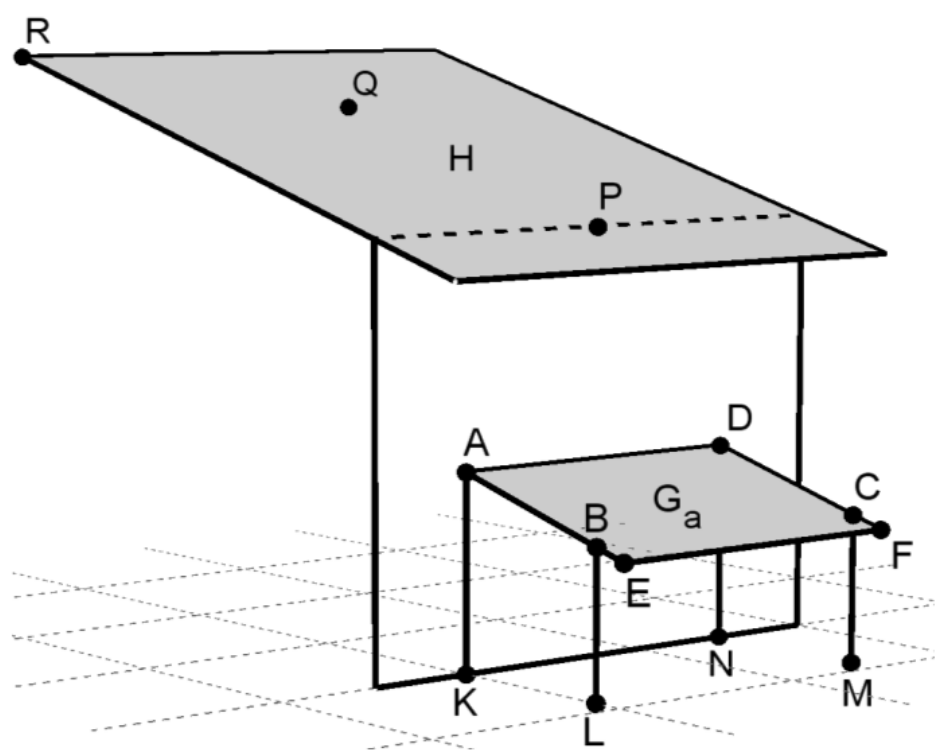
Das Dach eines Hauses liegt in einer Ebene \(H\). In einem kartesischen Koordinatensystem des \(\mathbb{R}^{3}\) ist die Ebene \(H\) durch die drei Punkte \(P(5;0;8)\) , \(Q(5;−7.2;10)\) und \(R(10;−10.8;11)\) festgelegt. Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden.
Aufgabe (a)¶
Ermitteln Sie jeweils eine Gleichung der Ebene \(H\) in Parameter- und Koordinatenform und beschreiben Sie deren besondere Lage im Koordinatensystem. [6]
Ergebnis
\(H:5x_{2}+18x_{3}=144\)
Aufgabe (b)¶
Die Größe des Neigungswinkels des Daches \(H\) gegen die Horizontale muss gemäß einer örtlichen Bauvorschrift mindestens \(15^{\circ}\) betragen. Zeigen Sie rechnerisch, dass die örtliche Bauvorschrift eingehalten wird. [3]
Aufgabe (c)¶
Zur Überdachung der Terrasse \(KLMN\) , die in der \(x_{1}x_{2}\)-Ebene liegt, wird ein rechteckiges Glasdach \(AEFD\) , dessen Neigungswinkel verstellbar ist, aufgebaut. Das Glasdach liegt in der Ebene \(G_{a}:(-1.8a+9.9)x_{1}+(36-6a)x_{2}+10.8x_{3}+14.4a=119.16\) mit dem Parameter \(a\in\mathbb{R}\) . Die Ebenen \(H\) und \(G_{a}\) sollen parallel zueinander liegen. Ermitteln Sie hieraus den Wert des zugehörigen Parameters \(a\) . [3]
Ergebnis
\(a=5.5\)
Aufgabe (d)¶
Zeigen Sie, dass die Punkte \(A(8;0;3.7)\) und \(B(8;3.42;2.75)\) in der Ebene \(G_{5.5}\) liegen. [2]
Aufgabe (e)¶
Nun nehmen wir die Punkte \(D(2;0;3.7)\) und \(K(8;0;0)\) dazu. Das Glasdach \(AEFD\) ist festgelegt durch die Punkte \(A\), \(E\) und \(D\) . Aus statischen Gründen darf die Glasüberdachung nur um maximal \(20~\%\) der Länge der Strecke \(\overline{AB}\) über den Punkt \(B\) hinausragen. Bestimmen Sie die Koordinaten des Punktes \(E\), wenn die maximal zulässige Länge vollständig ausgenutzt wird. [3]
Tipp
\(\left|\overrightarrow{AE}\right|=1.2\left|\overrightarrow{AB}\right|\)
Aufgabe (f)¶
Als Windschutz sollen die drei Seitenflächen \(AKLB\) , \(BLMC\) und \(DNMC\) verglast werden. Der umbaute Raum besitzt die Form eines geraden trapezförmigen Prismas. Geben Sie die Koordinaten des Punktes \(L\) an. Berechnen Sie die Materialkosten für die drei Seitenflächen, wenn der Preis \(200\) € pro \(1\,\mathrm{m^{2}}\) beträgt. [6]