Aufgaben¶
Aufgabe 1¶
Bestimmen Sie von folgenden Funktionen die erste und zweite Ableitung.
\(f_{1}(x)=\dfrac{4x}{3x^{2}+2}\) ; \(x\in\mathbb{R}\)
\(f_{2}(x)=\dfrac{3}{2x-5}\) ; \(x\neq\dfrac{5}{2}\)
\(f_{3}(x)=\dfrac{x^{2}-x+2}{x-2}\) ; \(x\neq2\)
\(f_{4}(x)=\frac{1}{2}x^{3}+2x^{2}-\frac{5}{3}x+1-\dfrac{3}{x^{2}+4}\) ; \(x\in\mathbb{R}\)
\(f_{5}(x)=\frac{3}{7}x+2-\dfrac{6}{(x-1)(x+3)}\) ; \(x\neq1\) und \(x\neq-3\)
\(f_{6}(x)=\dfrac{\frac{2}{3}x^{2}+\frac{1}{2}x-1}{x+2}\) ; \(x\neq-2\)
Aufgabe 2¶
Berechnen Sie folgende unbestimmte Integrale.
\(\int\dfrac{3}{(2x-1)^{2}}dx\)
\(\int\dfrac{4}{3x-7}dx\)
\(\int\dfrac{6x+5}{3x^{2}+5x-2}dx\)
\(\int(\frac{3}{2}x-1-\dfrac{2x}{3x^{2}-5})dx\)
\(\int(-2x+5)^{2}dx\)
\(\int\dfrac{2x^{2}+5x-1}{1-3x}dx\)
\(\int\dfrac{5x^{3}-3x^{2}-\frac{8}{3}x-\frac{10}{27}}{(2-3x)^{2}}dx\)
\(\int\dfrac{-\frac{1}{3}(x^{3}-4x^{2}-29x+39)}{(x-2)(x+4)}dx\)
Aufgabe 3¶
Gegeben ist die reelle Funktion \(f(x)=\frac{1}{3}\cdot\dfrac{x^{3}}{(x-1)^{2}}-2\) ; \(x\in\mathbb{R}\setminus\{1\}\).
Der Graph der Funktion \(f\) in einem kartesischen Koordinatensystem wird mit \(G_{f}\) bezeichnet.
Bestimmen Sie die Asymptoten von \(G_{f}\).
Untersuchen Sie die Monotonie von \(f\).
Bestimmen Sie Art und Koordinaten der Extrempunkte von \(G_{f}\).
Untersuchen Sie das Krümmungsverhalten von \(G_{f}\).
Berechnen Sie die Koordinaten der Wendepunkte von \(G_{f}\).
Untersuchen Sie, ob \(G_{f}\) gemeinsame Punkte mit seiner schrägen Asymptote hat.
Skizzieren Sie \(G_{f}\) mit Asymptoten in ein kartesisches Koordinatensystem.
Zeigen Sie, dass für \(f(x)\) gilt: \(f(x)=\frac{1}{3}x-\frac{4}{3}+\dfrac{1}{x-1}+\dfrac{1}{3(x-1)^{2}}\)
\(G_{f}\), die schräge Asymptote und die Ordinate schließen eine endliche Fläche ein. Berechnen Sie Flächenzahl dieser Fläche.
Aufgabe 4¶
Gegeben ist die reelle Funktion \(f(x)=\dfrac{x^{3}-9x}{x^{2}+1}\) mit \(x\in\mathbb{R}\).
Untersuchen Sie \(G_{f}\) auf Symmetrie zur \(y\)-Achse oder Ursprung.
Berechnen Sie die Nullstellen von \(f\).
Untersuchen Sie die Monotonie von \(f\). Runden Sie auf zwei Stellen nach dem Komma.
Ermitteln Sie Art und Koordinaten der Extrempunkte von \(G_{f}\).
Untersuchen Sie \(G_{f}\) auf Asymptoten.
Bestimmen Sie das Krümmungsverhalten und die Wendepunkte von \(G_{f}\).
Skizzieren Sie \(G_{f}\) in ein geeignetes Koordinatensystem.
\(G_{f}\) schließt mit der Abszisse zwei endliche Flächen ein. Berechnen Sie die Flächenzahl dieser Flächen gerundet auf zwei Stellen nach dem Komma.
Aufgabe 5¶
Gegeben ist die Funktion \(f(x)=\dfrac{x^{3}+x}{x^{2}-1}\) mit \(x\in D_{f}\).
Bestimmen Sie \(D_{f}\) und untersuchen Sie \(f\) auf Nullstellen.
Untersuchen Sie \(G_{f}\) auf Symmetrie zum Ursprung oder \(y\)-Achse.
Bestimmen Sie die Art und die Gleichungen der Asymptoten von \(G_{f}\).
Überprüfen Sie von welcher Seite aus sich \(G_{f}\) im Unendlichen an die schräge Asymptote annähert.
Bestimmen Sie die Art und die Koordinaten der Extrempunkte von \(G_{f}\).
Untersuchen Sie das Krümmungsverhalten von \(G_{f}\).
Skizzieren Sie \(G_f\) mit Asymptoten in ein geeignetes Koordinatensystem.
Die Parabel \(G_{p}\) hat ihren Scheitelpunkt auf der Geraden mit der Gleichung \(x=1\) und berührt \(G_{f}\) im Punkt \(Q(1.5;f(1.5))\). Ermitteln Sie den Term \(p(x)\).
Die Graphen \(G_{f}\) und \(G_{p}\) sowie die Abszisse und die Gerade mit den Gleichungen \(x=3\) schließen ein endliches Flächenstück ein. Markieren Sie die Kontur dieser Fläche in der Skizze und berechnen Sie die Flächenzahl dieser Fläche.
Aufgabe 6¶
Gegeben ist die reelle Funktion \(h:x\mapsto8\cdot\dfrac{2x^{2}-3x+1}{3x^{2}-2x+\frac{2}{3}}\) mit \(x\in D_{h}\). Der Graph von \(h\) in einem kartesischen Koordinatensystem wird mit \(G_{h}\) bezeichnet.
Bestimmen Sie \(D_{h}\) und die Nullstellen von \(h\).
Untersuchen Sie das Verhalten von \(h(x)\) an den Rändern des Definitionsbereichs und folgern Sie daraus auf eine Eigenschaft von \(G_{h}\).
Untersuchen Sie die Monotonie von \(G_{h}\).
Folgern Sie aus der Monotonie auf die Art und die Koordinaten der Extrempunkte von \(G_{h}\).
Gegeben ist weiter die Gerade mit der Gleichung \(t(x)=-\frac{32}{39}x+\frac{80}{13}\). Zeigen Sie, dass die Gerade \(G_{t}\) den Graphen \(G_{h}\) an der Stelle \(x=3\) schneidet.
Skizzieren Sie \(G_{h}\) mit Asymptote und \(G_{t}\) in ein geeignetes Koordinatensystem.
\(G_{h}\), \(G_{t}\) und die Asymptote begrenzen ein Flächenstück. Markieren Sie das Flächenstück mit einer dicken Kontur und berechnen Sie die Flächenzahl des Flächenstücks.
Aufgabe 7¶
Aufstellen des Funktionsterms aus gegebenen Eigenschaften
Bei folgenden Funktionen ist der Zähler- und der Nennergrad höchstens \(2\).
Die Funktion \(f\) hat die Polstelle 2. Ordnung \(x=2\). Die Nullstellen sind \(x_{1}=-2\) und \(x_{2}=1\). Eine Asymptote des Graphen hat die Gleichung \(y=2\).
Die Funktion \(g\) ist echt gebrochen-rational. \(G_{g}\) hat die Asymptoten mit den Gleichungen \(x=-2\) und \(x=1\). \(H(0;-2)\) ist relativer Extrempunkt von \(G_{g}\).
Der Graph \(G_{h}\) der Funktion \(h\) ist symmetrisch zur \(y\)-Achse und hat keine Definitionslücken. \(G_{h}\) hat die einzige Asymptote mit der Gleichung \(y=4\). Der Ursprung und der Punkt \(B(1;2)\) liegen auf \(G_{h}\).
Eine Ursprungsgerade und die \(y\)-Achse sind Asymptoten von \(G_{i}\). Die Tangente an \(G_{i}\) an der Stelle \(x=-2\) hat die Gleichung: \(t(x)=\frac{5}{2}x+2\).
\(G_{j}\) hat Asymptoten mit den Gleichungen \(y=-x-1\) und \(x=2\). Der Nenner von \(j(x)\) ist linear. An der Stelle \(x=-2\) hat \(G_{j}\) einen Extrempunkt.
\(G_{k}\) hat die Polstelle 2. Ordnung \(x=1\) und eine andere Asymptote hat die Gleichung \(y=1\). Die Funktion \(k\) hat die Nullstellen \(x_{1}=-3\) und \(x_{2}=5\).
Die Abszisse ist die einzige Asymptote von \(G_{l}\). \(G_{l}\) schneidet die \(x\)-Achse im Ursprung. Der Nenner hat die Form: \(x^{2}+a\) und es gibt keine Definitionslücken. An der Stelle \(x=1\) hat \(G_{l}\) die Steigung \(3\). \(G_{l}\) hat an der Stelle \(x=2\) einen Extrempunkt.
Der Graph der Funktion \(p\) hat eine horizontale Asymptote und zwei weitere Asymptoten mit den Gleichungen \(x=-2\) und \(x=1\). Die Normale an \(G_{p}\) an der Stelle \(x=0\) hat die Steigung \(\frac{8}{3}\). \(G_{p}\) verläuft durch den Punkt \(Q(2;\frac{15}{8})\) und schneidet seine horizontale Asymptote an der Stelle \(x=-1\).
Der Graph \(G_{v}\) der Funktion \(v\) hat als Asymptote eine Gerade, die mit der Steigung \(\frac{1}{3}\) fällt. Außerdem hat \(v\) die Polstellen 1. Ordnung \(x=-3\) und \(x=2\). Die Tangente an \(G_{v}\) an \(x=-2\) hat die Steigung \(\frac{5}{3}\) und verläuft durch den Punkt \(Z(4;10)\). An der Stelle \(x=-1\) hat \(v\) eine Extremstelle.
Aufgabe 8¶
Auf einem ebenen Gelände steht ein sehr hoher, zylinderförmiger Turm mit einem Innendurchmesser von \(5.0\,\mathrm{m}\). Durch das \(3.0\,\mathrm{m}\) hohe Tor soll eine möglichst lange, gerade Fahnenstange in das Innere des Turms gebracht werden. Im Folgenden soll ermittelt werden, wie lang eine solche Fahnenstange maximal sein darf.
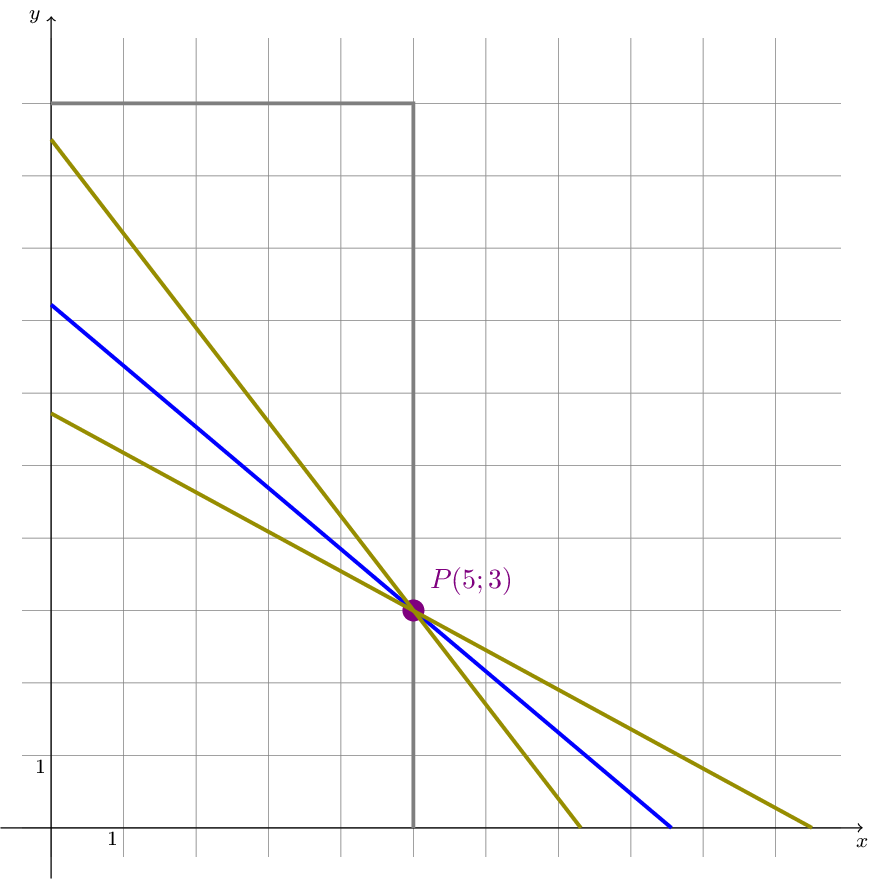
Wir betrachten dazu in einem Koordinatensystem die Menge der Geraden \(g_{m}\) mit der Steigung \(m\), \(m\in\mathbb{R}\) und \(m<0\), durch den Punkt \(P(5;3)\). Geben Sie die Gleichung einer solchen Geraden \(g_{m}\) in Abhängigkeit von \(m\) an.
Die Gerade \(g_{m}\) schneidet die \(x\)-Achse im Punkt \(A_{m}\) und die \(y\)-Achse im Punkt \(B_{m}\). Berechnen Sie die Koordinaten dieser Punkte in Abhängigkeit von \(m\).
Die Länge der von den beiden Punkten \(A_{m}\) und \(B_{m}\) begrenzten Strecke in Abhängigkeit von m wird mit \(l(m)\) bezeichnet. Zeigen Sie, dass für das Quadrat von \(l(m)\) gilt: \(l^{2}(m)=25m^{2}-30m+34+\dfrac{9-30m}{m^{2}}\) mit \(m<0\).
Die Fahnenstange darf höchstens so lang sein wie die kürzeste dieser Streckenlängen. Berechnen Sie \(m\) so, dass \(l^{2}(m)\) und damit auch \(l(m)\) seinen absolut kleinsten Wert annimmt, und ermitteln Sie damit die maximale Länge der Fahnenstange.
Aufgabe 9¶
Der Sicherheitsabstand \(s\) (in Meter), den zwei mit der Geschwindigkeit \(v\) (in Kilometer pro Stunde) fahrende Autos haben sollen, lässt sich durch den Funktionsterm: \(s(v)=\dfrac{v^{2}}{100}+\dfrac{v}{3.6}+6\) mit \(v\in\left]0;200\right]\) darstellen. Dabei ist \(\frac{v^{2}}{100}\) (in Meter) der Bremsweg, \(\frac{v}{3.6}\) der Reaktionsweg (in Meter) und \(6\) der Platzbedarf (in Meter) eines stehenden Autos. In einer Stunde legt ein Auto eine Strecke von \(1000\cdot v\) (in Meter) zurück. Die Funktion \(D\) gibt die Verkehrsdichte an, d.,h. die Anzahl der stündlich eine Messstelle passierenden Autos. Für \(D\) gilt: \(D(v)=\dfrac{1000\cdot v}{s(v)}\). Auf Benennungen wird bei der Rechnung verzichtet.
Geben Sie an wie sich Bremsweg und Reaktionsweg verändern, wenn die Geschwindigkeit eines Autos verdoppelt wird.
Berechnen Sie den Sicherheitsabstand sowie die Verkehrsdichte für \(v=50\) (Kilometer pro Stunde).
Ermitteln Sie die Geschwindigkeit \(v\), bei der die Verkehrsdichte \(D\) am größten ist.
Aufgabe 10¶
Eine Fabrik stellt Blechgefäße her, welche die Gestalt eines Zylinders mit einer aufgesetzten Halbkugel haben. Die Grundfläche des Zylinders ist ein Kreis mit Radius \(r\). Das Volumen eines solchen Gefäßes beträgt \(V=15\,\mathrm{dm^{3}}\). Die Dicke der Gefäßwand wird vernachlässigt.
Stellen Sie zunächst die Maßzahl \(O(r)\) der Oberfläche des Blechgefäßes in Abhängigkeit vom Radius \(r\) des Zylinders dar. Ermitteln Sie auch die Definitionsmenge der Funktion \(O\).
Berechnen Sie denjenigen Radius \(r\), für den der Materialverbrauch für diese Gefäße seinen absolut kleinsten Wert annimmt. Runden Sie Ihr Ergebnis auf drei Nachkommastellen.
Aufgabe 11¶
Eine gebrochen-rationale Funktion mit dem Term \(f(x)=\dfrac{ax}{x^{3}+b}\) in der größtmöglichen Definitionsmenge \(D_{f}\) hat folgende Eigenschaften:
Der Graph \(G_{f}\) der Funktion \(f\), besitzt im Punkt \(E(1;f(1))\) eine waagerechte Tangente.
\(G_{f}\) besitzt im Punkt \(N(-1;f(-1))\) eine Normale, die parallel zur Geraden mit der Gleichung \(y=-\frac{1}{48}x+7\) verläuft.
Bestimmen Sie einen möglichen Term \(f(x)\) der Funktion \(f\).
Untersuchen Sie das Monotonieverhalten der Funktion \(f\).
Skizzieren Sie einen möglichen Verlauf von \(G_{f}\).
Die Gerade mit der Gleichung \(x=u\) mit \(u\in\mathbb{R}^{+}\) schneidet die \(x\)-Achse im Punkt \(A_{u}\) und den Graphen \(G_{f}\) im Punkt \(B_{u}\). Die Punkte \(A_{u}\) und \(B_{u}\) bilden zusammen mit dem Punkt \(O(0;0)\) das Dreieck \(OA_{u}B_{u}\). Zeigen Sie, dass für die von \(u\) abhängige Flächenmaßzahl \(A(u)\) des Dreiecks \(OA_{u}B_{u}\) gilt: \(A(u)=\dfrac{6u^{2}}{u^{3}+2}\).
Ermitteln Sie denjenigen Wert von \(u\), für den die Flächenmaßzahl \(A(u)\) ihren absolut größten Wert annimmt und berechnen Sie diese größte Flächenmaßzahl.
Aufgabe 12¶
Gegeben ist die reelle Funktion \(g:x\mapsto\dfrac{-4x^{2}+24x-27}{2(x-3)^{2}}\) mit \(x\neq3\). Der Graph der Funktion \(g\) wird mit \(G_{g}\) bezeichnet.
Untersuchen Sie das Monotonieverhalten von \(G_{g}\).
Untersuchen Sie das Verhalten von \(g(x)\) an den Rändern des Definitionsbereichs und folgern Sie daraus auf Art und Gleichungen der Asymptoten von \(G_{g}\).
Berechnen Sie die Nullstellen von \(g\).
Skizzieren Sie \(G_{g}\) mit seinen Asymptoten in ein geeignetes kartesisches Koordinatensystem.
Die Vertikalen mit der Gleichungen \(x=a\) mit \(a<0\), \(x=\frac{3}{2}\), \(G_{g}\) und seine waagerechte Asymptote schließen ein endliches Flächenstück mit der Flächenzahl \(\frac{24}{11}\) ein. Berechnen Sie den Wert für \(a\).
Der Graph \(G_{g}\) wird nun im Koordinatensystem parallel so verschoben, dass die vertikale Asymptote die \(y\)-Achse und die horizontale Asymptote die \(x\)-Achse ist. Der neue Graph \(G_{p}\) ist der Graph der Funktion \(p\). Bestimmen Sie den Funktionsterm \(p(x)\) und untersuchen Sie \(G_{p}\) auf Symmetrie zum Ursprung oder \(y\)-Achse. Beschreiben Sie, welche Bedeutung das Ergebnis für den Graphen \(G_{g}\) hat.
Verbindet man den Punkt \(S(0;-\frac{7}{2})\) mit dem Punkt \(E(\frac{9}{2};0)\) von \(G_{g}\), so entsteht die Strecke \(\overline{SE}\). Die Parallele zur \(x\)-Achse durch \(S\) und die Parallele zur \(y\)-Achse durch \(E\) schneiden sich im Punkt \(Q\), der mit \(\overline{SE}\) ein Dreieck bildet. Zeichnen Sie das Dreieck \(SQE\) in die Skizze der vorherigen Aufgabe und berechnen Sie seine Flächenzahl \(A\).
Der Punkt \(S\) ist ein fester Punkt, während sich der Punkt \(E\) für \(x>3\) auf dem Graphen \(G_{g}\) bewegt. Dadurch bewegt sich der Punkt \(Q\) parallel zur \(x\)-Achse. An jeder Stelle \(x>3\) entsteht jeweils ein Dreieck. Berechnen Sie denjenigen Wert von \(x\), für den das entsprechende Dreieck die absolut kleinste Flächenzahl hat.